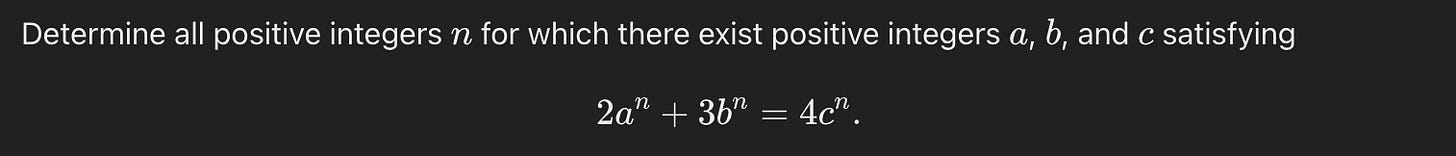Rate My Rate My Proof

An idea for a benchmark to see how well LLMs can spot flawed reasoning

I recently came across a thread where someone claimed that o1-pro had gotten a very high score on the Putnam Competition, a famously difficult college math competition. The author had posed the 2024 Putnam questions to o1-pro and graded its answers himself. However, it quickly became clear that he had misunderstood how solutions are graded in this competition. While some problems have concise final answers — e.g., “the only solution is n=1” — contestants are graded primarily on the proofs they write to justify those answers. If properly graded, o1’s score would have been low.

Evaluating proofs is a frustrating barrier to understanding LLMs’ math capabilities. Most mathematical activity involves proofs. LLMs can attempt to produce proofs. But we don’t have a way to tell if these proofs are any good — besides reading them. That’s fine for exploration but it’s a barrier to experimentation at scale.

From my own exploration, my sense is that LLMs exhibit proof-writing abilities comparable to the general mathematical abilities we’ve discussed here: they can execute on standard approaches but they don’t display much if any creative insight.

Still, wouldn’t it be interesting to give an LLM a large set of unsolved math problems — most of which require proof to resolve — just to see what it came up with? Well, it sounds interesting, but it would still be a slog to go over all those attempted proofs. Most of them would be junk; they might all be junk.

Although… we do have a hot new tool that helps slog through text. Could an LLM grade LLM proofs? Could it act as a first filter, at least getting rid of the obvious junk? I explored this a bit and saw at least a glimmer of ability, though I doubt it’s practically useful yet. But I do think we could add one more layer to the setup and make a benchmark to track how LLMs are progressing at proof-critiquing.

In the rest of this post I’ll discuss my exploration, and then outline the idea for this benchmark.

Rate My Proof

Since the Putnam kicked off this line of thinking, I decided to test LLM proof-critiquing on the first question from the 2024 Putnam. Here it is, followed by the solution.

Note that if there is any solution for a given n, then there must also be one with gcd(a,b,c)=1, because we can divide out common factors.

For n=1, it’s easy to find solutions, e.g. (1, 2, 2).

For n≥3, you can show there are no solutions like so. First, note that b must be even: otherwise the parity of the left- and right-hand sides won’t match. Then, taking the equation mod 4 shows that a must be even. Then, taking the equation mod 8 shows that c must be even. So gcd(a,b,c)≥2, contradiction.

For n=2, you have to proceed a bit differently. Looking mod 3 gives 2a² = c² (mod 3). Since squares are either 0 or 1 mod 3, this means both a and c must be divisible by 3. But now taking the equation mod 9 shows that b must be divisible by 3 as well. So gcd(a,b,c)≥3, contradiction. Done!

I presented the n≥3 case first because a parity argument is a natural place to start. You don’t think of it as “the n≥3 case” while you’re working it out. You just say, well, does the equation enforce anything mod 2? Yes, b must be even. Ok, what about mod 4? Ah, a must be even also. And mod 8? Ah, if n≥3, then c must be even too, contradiction. So you realize you need to treat n=2 separately. And you already tried mod 2, so you might as well try mod 3, and sure enough that works. If you’re not careful, though, you might not realize that the mod 2/4/8 argument only works for n≥3: you might think it works for n=2 also, and prematurely think you’re done.

This is exactly what o3-mini-high did: it claimed that the logic for n≥3 actually applies for n≥2, and thus missing the fact that n=2 needs special handling.

I doubt this is indicative of a deep limitation. If I pose the question restricted to n=2, o3-mini-high makes the correct mod 3 argument. I would guess that scaling up its “thinking time” would get it to the right answer overall.

But anyway, I was glad it gave this particular wrong answer because the error is very specific: its stated logic for n≥2 only applies for n≥3, and not for n=2. It’s a smoking gun to point to when critiquing the proof.

So, can o3-mini-high catch its own error? In a fresh chat, I gave it the same problem and the incorrect solution it had come up with. I included a short prompt explaining that this was a question from the Putnam together with one contestant’s solution, and I asked what score it thought the solution would receive.

I asked 4 times, and o3-mini-high gave itself a perfect score each time. For instance:

To be clear, it didn’t know that it was grading its own solution. Still, I wondered if somehow its own style “sounds good” to it. I don’t know how plausible that is, but I decided to give the same prompt to R1, i.e. have R1 grade o3-mini-high’s solution.

I asked 4 times, and R1 correctly identified the flaw 2/4 times! For instance:

Well done, R1.

I Grade You, You Grade Me

It’s a tangent, but of course I was curious about the reverse direction.

Does R1 grade its own wrong answers leniently, while o3-mini-high is more critical? Sure enough, though this case was a bit less clear: R1’s answer, while also inadequate as a proof, didn’t have such a smoking gun error. Instead, it just lacked (a lot of) detail.

Still, R1 gave itself a near-perfect score 4/4 times. For instance:

o3-mini-high objected more strenuously, also 4/4 times. Its harshest critique:

So, sure, maybe LLMs are worse at critiquing their own work and better at critiquing each other’s work. That’s a fun hypothesis, and could be useful in writing a proof-grading system, though I’m not getting my hopes up yet.

Rate My Rate My Proof

Back on the main thread, what stuck out to me was that once I knew the error in the proof, it was very easy to tell whether the LLM’s proof critique had found it.

So I wondered, given an answer key specifying the correct critique of the proof, could a third LLM assess whether the second LLM had correctly found the errors in the first LLM’s proof? (Are you enjoying the recursion?)

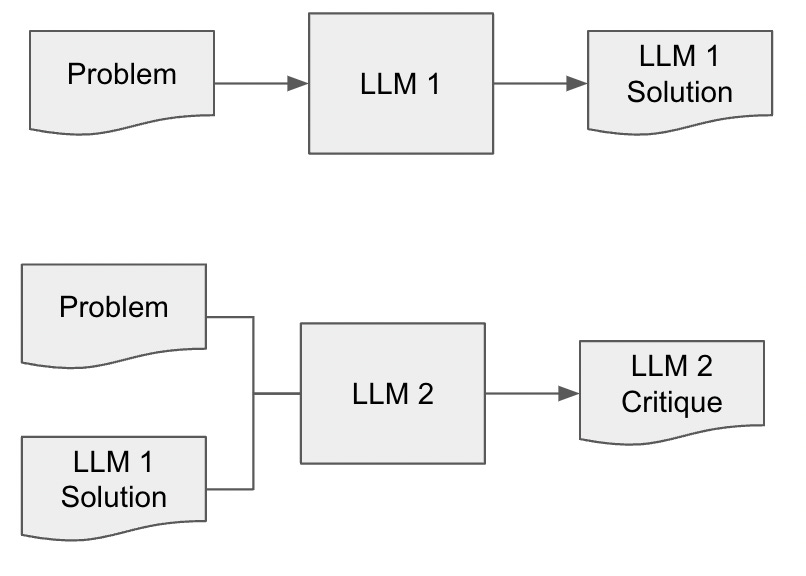
A diagram makes this clearer. First, below, we have the setup where an LLM tries to solve a problem and a second LLM, whether an instance of the same model or a different model, tries to critique it.

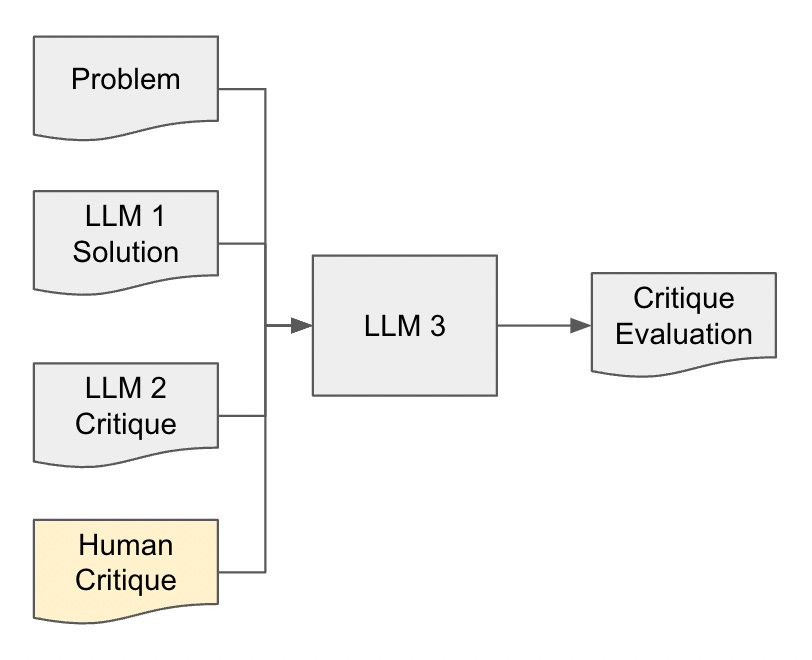
But then, could we add a third LLM, give it the target critique, and have it evaluate the second LLM’s critique against this?

Why would we want to do this? It would benchmark to what extent LLMs are capable of critiquing proofs. From what I’ve seen, I am guessing that they’re not so good at it today. Maybe if you have different models critique each others’ proofs you can get somewhere, but I bet not too far.

However, if LLMs showed progress on such a benchmark, we would be encouraged to try them on relevant tasks. Maybe throwing 1000 unsolved math problems at an LLM, and having an LLM filter the results, wouldn’t be such a waste of time. Also, mathematicians need to check proofs all the time: their own work, the work of their collaborators, papers they are refereeing, and so on. It would be great if LLMs could help with that, and it would be useful to have some indication of their readiness.

Furthermore, I suspect a similar setup could judge the readiness of LLMs for critiquing work in other fields where rigorous reasoning also plays a role, like law, finance, or science. Math is at an extreme in having black-and-white judgements about the correctness of its arguments, but there are surely some “smoking gun” kinds of errors in legal and scientific writing as well.

I think a good question to ask when considering a benchmark is, were an AI system to score perfectly on the benchmark, would you feel the urge to downplay the result? If the answer is yes, you should consider whether you think the benchmark is really measuring anything at all. In this case, I think I wouldn’t downplay success: if an AI system is spotting proof errors comparable to a human-written gold standard, I’d say so much the better for the system.

The only open question, I think, would be whether the benchmark was comprehensive enough to capture the multitude of ways proofs can be inadequate, so that the system’s performance would generalize to practical applications. You’d hope, though, that broad data collection could mitigate that problem.

Anyway, lest we get ahead of ourselves: does this benchmark idea work at all? Can LLMs which aren’t good at grading proofs nonetheless grade gradings of proofs, if given an answer key?

I tried this out with the following prompt.

Please evaluate whether a trainee grader's evaluation of a solution to a math problem correctly matches an expert grader's evaluation of the same solution.

Here is the math problem:

{Problem}

Here is the solution being graded:

{Solution from LLM 1}

Here is an expert grader's evaluation of the solution:

{Evaluation from me}

Here is a trainee grader's evaluation of the solution:

{Evaluation from LLM 2}

Please use the following scale to state whether the trainee grader's evaluation of the solution matches the expert grader's evaluation of the solution.

4. The trainee's evaluation largely matches the expert's evaluation.

3. The trainee's evaluation substantially matches the expert's evaluation, differing only in minor details.

2. The trainee's evaluation only partially matches the expert's evaluation, either including substantially distinct elements or omitting key elements of the expert's evaluation.

1. The trainee's evaluation largely does not match the expert's evaluation.

I selected one of o3-mini-high’s incorrect self-evaluations, as well as one of R1’s correct evaluations of o3-mini-high’s solution. I gave the whole prompt to o3-mini-high. And, sure enough, o3-mini-high recognizes that R1’s correct proof evaluation matches mine much better than its own proof evaluation does. Specifically: it gave R1’s evaluation an average of 3.75 on the scale, vs. straight 1’s for its own evaluation (4 samples each).

This is what I’d expect here: it isn’t a particularly hard case. In fact, I got similar results giving the prompt to 4o, suggesting the task doesn’t need too much “reasoning”, at least on this one easy example. But it’s good to see that there isn’t some sort of cognitive dissonance forcing OpenAI models to recognize and prefer their own work.

So I think that’s interesting: we might be able to set up a benchmark that will let us automatically track LLM progress on identifying flaws in proofs.

I’d love to push this forward. Do you have any examples of flawed proofs that you’ve come across, even subtly flawed ones? Please share if so!