Two topics in today’s post.
I’ve been writing about how current models may have a “creativity deficit” when it comes to math problems. What on earth does that mean? I’ll begin to discuss this, though surely won’t fully answer it. My ultimate goal here is to be able to operationalize some notion of creativity into a practical benchmark.
I’ll review a few problems from recent math competitions where I thought the top models showed an interesting mix of success and failure. My goal here is to continue getting a handle on where the frontier lies, as well as to have fun with math problems.
What is Creativity?
Epistemic status: you gotta start somewhere!
The consensus in psychology seems to be that creativity means coming up with ideas that are novel and useful. Since we’re talking about solutions to math problems, we can presume usefulness: an idea is useful if it helps solve the problem. So we’re left to analyze novelty.
An idea’s novelty is judged relative to an implicit background of existing ideas. This can be hard to do in practice when judging the work of another agent, since you don’t know the contents of their background.1 But, conceptually, we should assume a fixed background.
So, holding the background fixed, what makes an idea novel? Even if an idea doesn’t literally appear in the background, we may still classify it as a “straightforward elaboration” of known ideas, and thus not consider it novel. Algorithms are an extreme case: the rote application of an algorithm to solve a problem, even a problem that hasn’t literally appeared before, is not novel.2
We might phrase the rote nature of algorithms as being about predictability: in an algorithm, you always know what comes next. So, perhaps a key element of creativity is not being able to predict what comes next. I don’t know much about information theory, but this reminds me of Shannon’s empirical measurements of the information density of English.3 Subjects were asked to guess the next letter in a sentence, given only the letters preceding it. Below is an example from the paper.

The letters ‘R’ and ‘V’ in “reverse” required the most guesses by far: these letters convey something new about what the sentence is saying. In other words, they have high information density.
I think creative solutions have something in common with this. Authors often highlight the moment where they are about to present a high information density idea with phrases like, “The key idea is …” Once you have stated the creative insight, you “only” need background and “straightforward elaboration” to solve the problem. In other words, the novelty of a solution is closely related to the solution’s information density relative to the background.
For easier problems, there may be no “key idea” at all: it’s all in the background. For problems requiring a single insight, the key idea might be stated concisely. (In this example, it’s just “Stewart’s theorem”.) For harder problems, a concise statement may not be possible. Perhaps the problem requires the conjunction of several unrelated key ideas. In extreme cases, the “key idea” might not be possible to express any less concisely than a hierarchical outline of an entire research program.
I wonder if this hints in a direction that might be ever-so-slightly operationalizable. The idea would be, for a given model, you want to find the most concise “key idea” statement which you can give to the model as a hint, and with which it could solve the problem, perhaps within a fixed amount of time. The length of that hint would measure the novelty of the solution, at least relative to that model’s background.
If that pans out, it’s a short step back to creativity. As discussed in the comments on the previous post, creativity seems analogous to a search through the space of ideas. Loosely speaking, the bigger a statement is, the harder it is to find. Thus, the more novel the solution, the more creativity required to find it. So, a model would be creative to the extent it could find novel solutions without hints, given enough time.
That’s a start, anyway. It’s funny, in writing a blog about math and AI — two areas in which I’m not at all an expert — this discussion of creativity has me feeling the most out of my depth. Sound off in the comments with your own thoughts on what creativity means and how we might measure it!
Error Analysis Roundup
If you spend enough time online, you’ll see funny examples of LLMs getting things wrong. (I post some myself.) But the selection effect is so strong that it’s hard to draw any conclusions: only the juicy ones make it onto your feed. This is something I really appreciate about MathArena: as math competitions keep happening, we can get a fresh sample of AI math performance free from this bias. I plan to use this to do occasional roundups of problems where I find the models’ performance noteworthy in some way. Sorry, you’re still subject to the selection effect of what I find interesting!
Today I’ve selected four problems from the Harvard-MIT Math Tournament (HMMT), which took place last week. The problems come from the Individual Round, which consists of three 50-minute 10-problem tests, split by subject area (algebra / number theory, combinatorics, and geometry). Problems are ordered by difficulty, generally comparable to mid-to-high level AIME problems.
o3-mini-high leads the field by a sizable margin, so we’ll focus on its answers.

Roundup Updates
Here are my take-aways from the selected problems.
We know models make “careless” mistakes sometimes, but on Algebra 3 we see it falling into the slightly more interesting failure mode of being too enamored with a clever idea and getting stuck down a rabbit hole.
It has a glimmer of creativity on Algebra 7, where it manages to see the hidden trigonometric substitution 1/4 times. Interestingly, given the concise hint to “try a trigonometric substitution” it gets perfect performance.
Combinatorics 4 seems too hard for it at the moment, and we wonder if that’s because the solution relies on a visual aid. A much less concise hint helps here, but the hint may give away too much.
It seems like a one-trick pony on geometry: coordinates or bust. Problems like Geometry 5, which require introducing new geometric elements to the picture, seem beyond it.
If you’d like to read some-but-not-all of what follows, I thought Algebra 7 and Combinatorics 4 were the most interesting.
Algebra 3
With problems ordered roughly by difficulty, it’s notable that o3-mini-high got the third problem wrong 4/4 times. What’s more, it got the same wrong answer each time. From what I’ve seen, this is unusual: when the models don’t know how to solve a problem, they generally give a range of wrong answers.
Here’s the problem:
You might be tempted to try something a bit fancy here, like the AM-GM inequality. But it turns out the right path is just to do what’s obvious: you have three equations and three unknowns, you can just solve. Here’s the solution.
Take log₂ of all the equations, and write a = log₂x, b = log₂y, and c = log₂z. We want to minimize a+b+c. For brevity, write log₂3 = k. We then have this system:
Add two equations and subtract the third to isolate the product terms:
Multiply two equations and divide by the third to isolate the squares:
The above steps are labor-saving, but you can also just isolate variables and substitute by rote. Either way, taking square roots — specifically the negative roots, as we’re looking to minimize a+b+c — and unwinding the variable substitutions gives the correct answer of 1/576.
o3-mini-high always answers 576. That corresponds to taking the positive roots. How odd: I’ve seen it make careless mistakes, but usually not this careless; and I’ve never seen it make a careless mistake with this kind of regularity.
Briefly, what about the other models? In the MathArena data, o1 got it right 2/4 times, and only gives 576 for one of its wrong answers. gemini-flash-thinking got it right 4/4 times. All correct solutions followed the above outline, sometimes with messier algebra around substituting variables, but the same basic flow.
So what’s going on with o3-mini-high? It seems like it really wants to make the substitution S = a+b+c. This is a very reasonable idea, but in this problem it takes you down a dead end. o3-mini-high gets to a point where it has an equation it can’t solve systematically, but it can guess a solution. Unfortunately, the easier-to-guess solution corresponds to the positive roots. Here’s one example of that:
But other times it really does seem to have the solution right in front of it. Here it is breezily ignoring the negative roots:
I tried to give it slightly different problems to see how stable this error is. It still messes up if given the a(b+c) / b(a+c) / c(a+b) set of equations to begin with, but it’s reliable again if given the ab / bc / ac set of equations. This latter case still requires it to consider negative roots, but I think it’s less tempted to use the S = a+b+c substitution when the problem is presented in that form. It also seems reliable again if the constants are simpler. E.g., if the a(b+c) set of equations equals 2, 3, and 4 then it gets the right answer. I generally didn’t find a smoking gun: give it enough hints, or perturb the problem enough, and it gets back on track.
The boring-but-correct thing to say here is that we’ve just stumbled upon a random corner of math-space where o3-mini-high is disposed to make a mistake. We know such corners exist, so we shouldn’t make too much of finding one. Even human cognition works this way, e.g. optical illusions.
There’s one more thing to say, though. o3-mini-high’s problem seems to be that it knows more problem-solving strategies, and thus can be tempted into trying something too fancy and getting bogged down. (Very relatable!) Contrast this with gemini-flash-thinking, which is in general much worse at math competitions, but aced this question: I assume that’s because it could only do the obvious thing, and that worked in this case. This is an inverse of “when all you have is a hammer”: the more tools you have, the harder it is to pick the right one.
One thing we might expect from future models, then, is a bit more emphasis on recognizing when they are stuck and trying to approach the problem in a new way: we’ve seen examples of this in some chains-of-thought, but they could clearly go further. It’s certainly the sort of thing you could imagine “scaling test-time compute” to take care of eventually, though I don’t know how easy it will be to get models to strike an efficient explore/exploit balance when trying to solve hard problems.
Algebra 7
This problem is similar to one we discussed here in that the algebra hides a geometric relationship. The solution is to realize that a, b, c are the cotangents of the three angles in a triangle. Here’s the full solution.
There’s a purely algebraic solution as well, but the geometric solution is what you’re “supposed” to find. And, o3-mini-high got the geometric solution once! Its other three attempts weren’t on the right track. A few other models got the right answer once or twice, but only because they seemed to luck into the right algebraic path to follow.4
This shows that the current models can sometimes hit on a creative solution, at least if the key idea isn’t too complicated. Indeed, when I added, “Hint: use a trigonometric substitution.” to the problem statement, o3-mini-high got it right 4/4 times. This is a bit of validation for the ideas discussed in the Creativity section: this problem requires just that much creativity, relative to o3-mini-high’s background and elaboration capabilities.
Presumably this is a case where scaling test-time compute will help, though the search space grows exponentially with the length of the required creative insight.
Combinatorics 4
Basically no model solved this problem. o3-mini-high got the right answer once, but its explanation suggests it just got lucky.
Here’s the problem:
The solution can be presented as a preliminary observation plus a key insight.
The preliminary observation is to note that the first two moves (“up” and “right”) increase the sum of the coordinates by 1, whereas the second two moves (“up-left” and “down-right”) leave this sum unchanged. Thus, any valid path from (0, 0) to (3, 3) will have precisely six total “up” and “right” moves. This is a standard approach: when a problem describes a dynamic, look for how things do or don’t change as the dynamic evolves. o3-mini-high made this observation once but then got stuck.
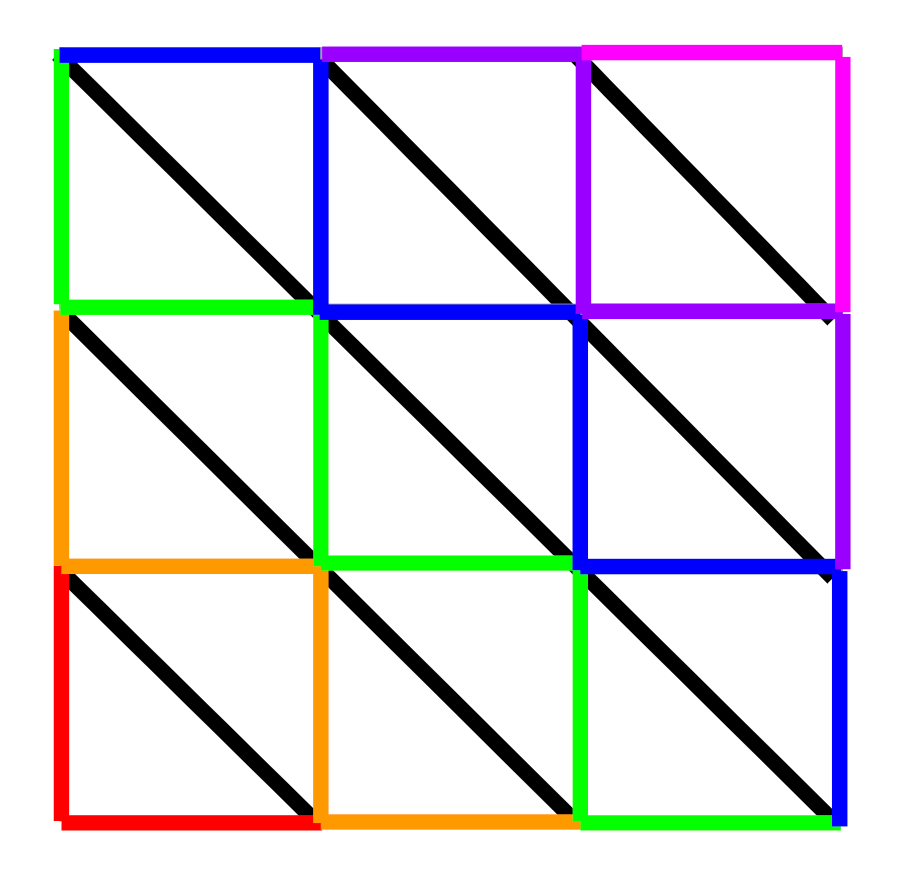
The key insight builds on this. It’s easiest to explain with a diagram like the one below. The “up” and “right” moves are drawn with different colors based on their starting and ending coordinate sums: red goes from 0 to 1, orange from 1 to 2, etc. The “up-left” and “down-right” moves are all black. The key insight is that, not only will any valid path contain six total “up” and “right” moves: it will contain exactly one move from each color. To finish, we need to note that any such selection, i.e. any set of one red, one orange, etc. fully determines which diagonal moves are included: you slide along the diagonal from the end of one color you’ve chosen to the beginning of the next.
The answer is the product of the number of segments of each color: 2*4*6*6*4*2.
Why is this beyond the models? I wonder if it’s because they can’t use the diagram. Note how much my explanation above relies on it. Really, I was tempted to write less and just say, “Stare at the diagram until this becomes clear.” Putting it all into text is a lot less efficient, at least for humans.
I think “geometric bookkeeping for combinatorics problems” is an interesting frontier. Problem 3 on the 2024 IMO fits this bill, see e.g. this great write-up. Even AlphaProof didn’t get that one. I wonder how much training on human-written chains of thought, or, more tantalizingly, human-drawn diagrams, might help the models here.
I was able to write a hint that got o3-mini-high to perfect performance on this problem, but I don’t find it satisfying.
Hint: Note that first two moves increase the sum of the coordinates by 1, while the second two moves leave the sum unchanged. Show that a path is uniquely determined by an independent choice of: one move that takes the sum from 0 to 1, one move that takes the sum from 1 to 2, etc. Then count the total number of 0->1 moves, total number of 1->2 moves, and so on.
In addition to being long, I worry this gives too much away. It’s a bit like saying, “The answer is 2*4*6*6*4*2.” Nothing forces the model to actually “show” the suggested fact. But I didn’t find anything else that worked. Can you do better? Give it a try! Copyable text of the problem is in this footnote.5
Geometry 5
Speaking of geometry, my running hypothesis is that the models’ two tools for solving geometry problems are applying known formulas and using coordinates. This is born out in the HMMT questions: o3-mini-high freakin’ loves coordinates. Almost none of the human-written solutions involve coordinates, and the few that do use them sparingly. But o3-mini-high always uses coordinates.
What does a problem look like that can’t be solved with coordinates? Here’s one that o3-mini-high got only once, and which no other model got at all. I can’t tell from its explanation where o3-mini-high was completely lucky, or else lucked into a correct algebraic path from its coordinates — but its solution is certainly not insightful.
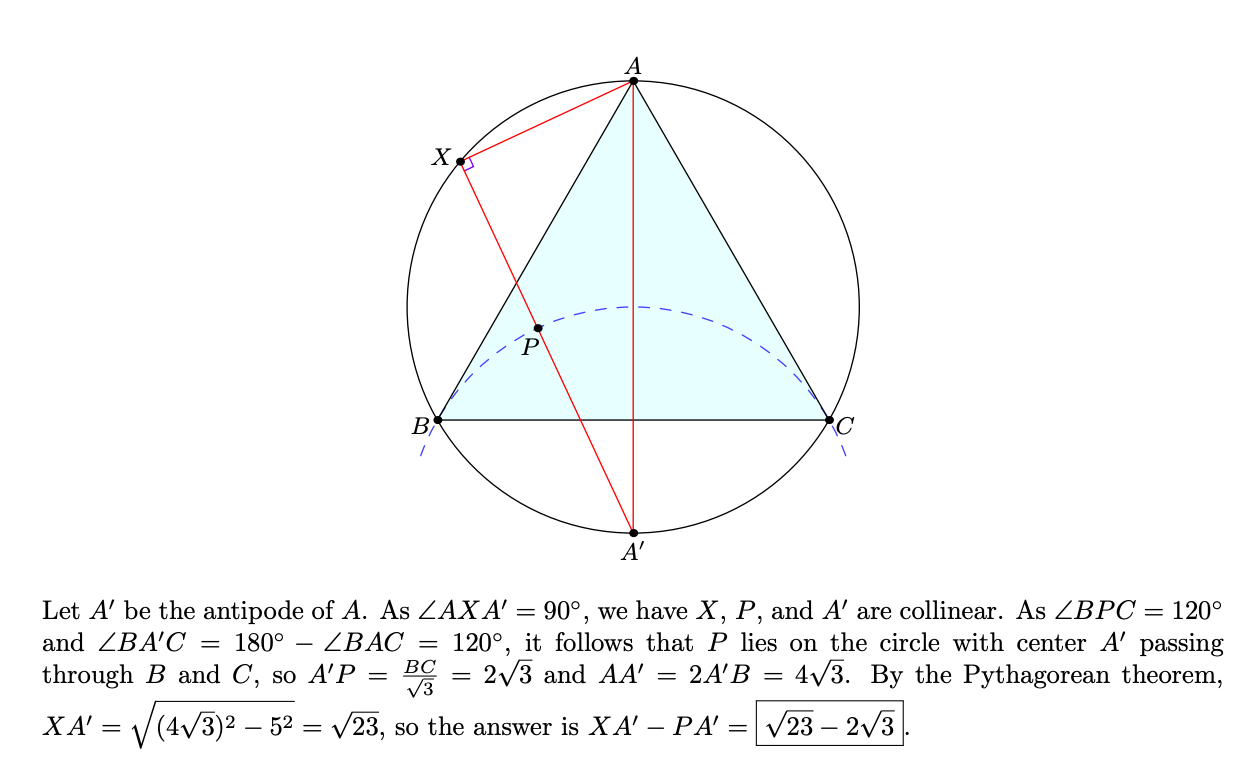
The insightful solution introduces the point opposite A on the circumcircle:
This is often the key to geometry problems: you add elements (points, line extensions, circles) that make it easier to establish relationships. It’s just a guess, but I suspect this is what AlphaGeometry got good at: adding the right elements. From what little I know, it seems like a decent fit for that architecture. I don’t see any reason why this can’t be trained into LLM-based systems in principle, though again it’s unclear what kind of training data would be most efficient.
Giving o3-mini-high the hint to introduce A’ as the antipode of A didn’t seem to help it, though I didn’t try too hard. Again feel free to try for yourself!6
Recently I was speaking with someone and I quoted a line from a movie. I wrongly assumed he had seen the movie. He hadn’t, but he really liked the line! (It was from the boardroom scene in Margin Call, where the CEO says, “There are three ways to make a living in this business: be first, be smarter, or cheat.”) Before I clarified, it was clear he thought I’d made a creative observation. Really I was just repeating someone else’s creativity: the idea was in my background.
Although, it may be creative to realize that, upon reformulating a problem, a known algorithm now applies to it.
“Language models” in their infancy!
The one exception is R1, though you wouldn’t know it from its summarized solution. But, looking into its chain of thought, sure enough it eventually hit on the right trigonometric substitution. Sometimes when a model seems to pull the right answer out of thin air, it actually did get it for the right reason!
Sophie is at (0,0) on a coordinate grid and would like to get to (3,3). If Sophie is at (x,y), in a single step she can move to one of (x+1,y), (x,y+1), (x−1,y+1), or (x+1,y−1). She cannot revisit any points along her path, and neither her x-coordinate nor her y-coordinate can ever be less than 0 or greater than 3. Compute the number of ways for Sophie to reach (3,3).
Let △ABC be an equilateral triangle with side length 6. Let P be a point inside triangle △ABC such that ∠BPC=120∘. The circle with diameter AP meets the circumcircle of △ABC again at X≠A. Given that AX=5, compute XP.









I found this an informative and enjoyable read. I wrote down some thoughts about your account of creativity, and an alternative suggestion, here:
https://docs.google.com/document/d/1PVxMSnvmQo2iWFGqzZ2_Bhgbgdm_7MP9ojkqdTFl3ng/edit?usp=sharing