Who Needs Insight When You've Got Speed
Do AI systems have a creativity deficit?
In my previous post I discussed how part of what makes the AIME a difficult math test for humans is that it is timed. In this post I’ll look at two cases where AI systems solve AIME-style problems in ways that a human probably wouldn’t be able to pursue due to the time constraints. I’ll also look at a similar case where they still fail outright.
My emerging impression of these AI systems is that they are like a human who
is bright but not brilliant,
has access to Wikipedia and textbooks,
has very high patience and diligence, and
works very quickly.
In other words, they are fast but not that insightful. This is interesting, because some AIME problems are designed to require insight: there’s a key observation that unlocks a quick solution to the problem, but that observation can be difficult to spot. Such problems often have less-insightful approaches available as well, but contestants try to avoid these because they are slower and more error-prone. In the worst cases, they aren’t even really guaranteed to give the right answer and are just a way of making an educated guess.
These approaches don’t amount to full-on brute-force search: they are more about picking up on a simple pattern and hoping it works out. Humans do this too, given time: it’s a good way to guess the answer, and then you can try to back your way into the real insight. But my guess is that top AIME performers aren’t taking these routes.
This means we can’t extrapolate an AI system’s abilities as cleanly as we might hope: a human needs insight to get harder AIME problems in time; not so for an AI system.
Even for the best current AI systems, this approach still only works sometimes. In this post I’ll look at three AIME-style questions, all with a similar flavor. The AI systems always get the first, sometimes get the second, and never get the third. I’ll discuss a bit at the end what this means for AI evaluation.
Warning: solutions are shown shortly after the problem statement, so scroll carefully if you want to try a problem on your own first.
Just Find the Pattern
Our first example is Problem 11 on the 2024 AIME II.
This problem hinges on finding a helpful factorization, which imposes strong constraints on valid triples. At least to my eyes, though, it’s not easy to find. Here’s one way to derive it. First, note that:
Using the two conditions from the problem and dividing by 3 gives us:
Now comes the part that is a bit out of nowhere. Consider:
Combining the previous two equations and using a+b+c=300 again, we have:
That’s the key: it means that at least one of a, b, and c must be 100. It’s then easy to check that there are no other constraints: if one of the numbers is 100, then the other two can be any pair of non-negative numbers that add up to 200. For each of a,b,c being 100, there are 201 possible pairs for the other two. This triple-counts (100, 100, 100), so the answer is 201*3 - 2 = 601.
R1 gets this question right, but, thanks to us being able to see its chain of thought, we can see that it doesn’t find the key factorization. Here’s what it does instead.
It manipulates the given constraints for a while but fails to find anything helpful.
It tries plugging in some specific values and notices that (100, 100, 100), (0, 100, 200), and (50, 100, 150) all work.
It decides to consider the case where one variables is equal to 100, and proves that this gives rise to 601 solutions.
It then tries six triples where no variable is equal to 100, and shows that none are solutions.
It then says, “Hmm, interesting. It seems that when variables are close to 100, the value [of 100(ab + bc + ca) - abc] is very close to 2,000,000. But maybe exact solutions only occur when one variable is 100.”
But it doesn’t prove this. It just wraps up and gives the correct answer.
As usual: that’s very relatable! It’s a totally valid way to guess the answer, and it would even get full credit on the AIME. But it’s a bit risky, because it doesn’t prove that one of the variables must be 100. It might be missing something. Since this approach would be time-consuming for a human on the clock (you have to work out lots of examples), and might yield the wrong answer, I wouldn’t expect most contestants to see it through.
o1 is similar to R1, though with less transparency. Here, for instance, is its argument that there are no other solutions. I suspect it’s basically the same under the hood.
Overall I was a bit surprised by this: it seems like the level of diligence that o1/R1 are applying might be enough to solve the problem fully, if they just spent their time on algebraic manipulations instead. Sure enough, o3-mini-high seems to find the factorization every time. So, at least for this problem, the point isn’t that this is an exceedingly hard factorization to find, but that R1/o1 can find the answer in a way that humans probably wouldn’t do, at least not while on the clock.
Where’s the Fun in That?
Our second and third examples come from the OTIS Mock AIME 2025: an AIME practice test developed by math olympiad coach Evan Chen. Chen developed two tests this year: one is a bit harder than a typical AIME and, to math olympiad veterans, is a bit more fun and interesting. Both examples come from the first one, and are listed as two of Chen’s favorites.
Maybe It’s Nice?
The solution revolves around an insight which takes a bit of a eureka moment to find. That’s what makes this problem harder than usual for the AIME, and I also imagine that’s why it’s one of Chen’s favorites: it’s very satisfying if you do find it.
Here’s the solution:
R1 doesn’t seem able to get this question, which is a shame as its chain of thought would be interesting. o3-mini-high gets it some of the time, but again not via the intended insight. Instead, it seems to pull the solution out of thin air, usually first finding the value for c. Without access to the chain of thought, we have to resort to asking it how it found this value, and we don’t know if it’s reporting accurately. It does tend to say the same thing across answers, at least. For instance:
What it means about “leading to a factorable equation for a and b” is that, if 1/a+1/b=1/d, then (a-d)(b-d)=d^2 and, after finding the prime factors of d, this is manageable to solve. Essentially: it hoped the problem would work out nicely, and spent some time testing just in case. That’s not guaranteed: just because the reciprocals of a, b, and c sum to an integer doesn’t mean some two of them do as well. But it just so happens to work for c in this case.1 In fact, o3-mini-high appears to be sensitive to the wording: the problem was originally worded to ask for a, but if you instead ask for c it gets the right answer much more reliably.
If you weren’t on the clock, you might as well try this approach and see. But if you were taking the AIME under time pressure, this would be something of a desperate move: it might just waste your precious time. For an AI system, though, why not? Even if it were aware of the time pressure, it has the speed to try approaches that are merely worth a shot.
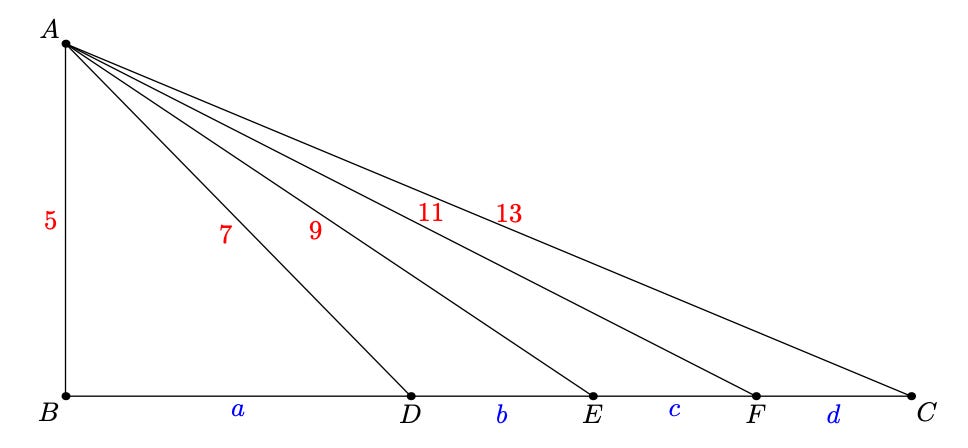
You Must See the Equations
I imagine this is a bit of a polarizing problem: some might find it compelling, others exasperating. Presumably Chen is among the former. The insight here is that these equations are a geometry problem in disguise. The first three equations are what you get if you apply Stewart’s theorem to this diagram, and the last equation says that BC=12.
If you recognize that, the problem is easy. Big if!
None of the AI systems get it, nor do they come particularly close. That’s even though the problem is open to less insightful approaches: after all, it’s just a system of four equations with four unknowns. But whatever approaches they try don’t pan out.
And the Scales Fell From Its Eyes
These examples should adjust our estimation of current AI capabilities a bit: the systems are relying more on speed and less on insight, compared to humans. It also shows that some problems are resistant to these less-insightful approaches, at least for the moment.
Do these insight-driven problems suggest a deeper limitation to AI systems? I would be surprised if these specific problems did. It seems to me that the relevant insights can be expressed fairly concisely: “try expressing 1/315 using partial fractions” or “consider Stewart’s theorem” are pretty good hints. I think that gives some hope that a similar AI system, just working 10x as fast and considering 10x as many ideas, would be able to hit on the key insights. Then again, giving those hints to the AI systems today doesn’t help them find the key insights, so maybe I’m overestimating their value.
Regardless, I think this points the way to an interesting benchmark: the current AI systems seem to have a bit of a creativity deficit vs. humans when it comes to problem-solving, so it would be very interesting to measure them purely on problems where the only path to a solution requires a key insight.
Thanks to Dave Savitt for discussion on this point.


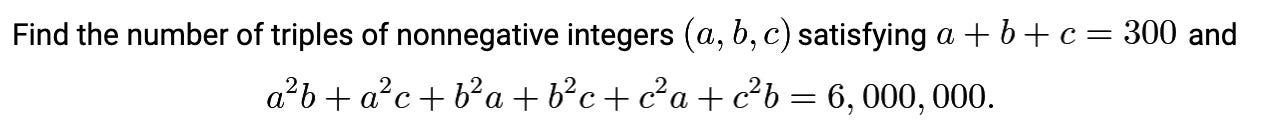

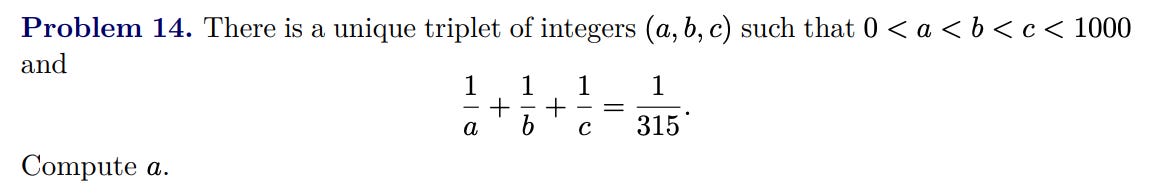



As you know, I’m an investment researcher, and I recently started asking for “deep research” reports on all my questions before we humans tackled them. My version of what you describe the as the creativity deficit: I’ve been disappointed on how its answers reflect back conventional wisdom: confidence that US stocks are better investments than other countries. Same with US growth.
There’s a phenomenon in finance we sometimes call the davos effect - whatever the elite consensus is in Davos, the opposite tends to happen (eg 2022 everyone in Davos was talking about stagflation risks, then the opposite happened). That was sort of my reaction to many investment research questions. (If it’s a prediction, bet on the opposite).
Of course, the vast majority of humans have the exact same problem and bias.
On the other hand, its ability to answer more factual and contained questions is really impressive, so don’t read this as me being a skeptic!