Contra Benchmark Heterogeneity
Why I'm lukewarm on Humanity's Last Exam
I’ve been beating a drum about AI benchmarks. I think a requirement for benchmarks is that, if an AI system does well on a benchmark, it should be clear what that means. In other words, benchmark performance should have a greater implication. This may sound obvious, but I think it’s rarely the case. More often, I think benchmarks are designed ad hoc to stump current AI systems. Then, when a new system comes along and does better, we don’t know what to make of it. There’s no “so what” for most benchmarks.
In this post, I’ll discuss what makes for good benchmarks in general. Then I’ll focus on one mistake I think many benchmarks make today: their contents are extremely heterogeneous, which makes it difficult to interpret performance. As an example, I’ll look in detail at a recently-released benchmark called Humanity’s Last Exam.
TL;DR
Benchmarks. It would be great if benchmarks predicted success at some practical task. For humans this can be done, at least in some domains, using academic-style tests. However, this relies on correlations in humans between test performance and practical performance, and we can’t rely on the same correlations in AI systems. Full-on simulation of the relevant task would be ideal for AI systems, but it will take significant investment to get there. In the mean-time, we can use academic-style tests for AI systems, but we should keep them narrowly targeted so we can keep a handle on what they measure.
Humanity’s Last Exam. This benchmark is anything but narrow. It covers “dozens” or “hundreds” of subjects, although 41% of its questions are in math. After going over its basic design, I delve into a random sample of 10 math questions. I find an extremely heterogeneous mix: easier-than-AIME geometry problems, problems that mostly just require finding the right Wikipedia page or the right theorem in a paper, a hard homework exercise from an upper-level undergraduate class, and more. My summary is that the benchmark is all over the place, and that performance on it will be hard to interpret. I conclude by discussing how it could be improved by splitting into multiple better-targeted benchmarks.
Marking the Benchmarks
School Tests
It takes a lot of effort to make tests meaningful for humans. For instance, the legal profession invests significantly in constructing the LSAT. This effort apparently pays off: the profession seems confident that LSAT performance is a strong indicator of having the skills required for success as a lawyer. Indeed, law school admissions hinge to a great degree on LSAT scores, despite the fact that legal work doesn’t superficially resemble taking the LSAT.
This relies on correlations in human abilities: the same cognitive skills that are used on LSAT reading comprehension questions might also be used when, say, analyzing a carefully-worded contract. Unfortunately for AI researchers, AI systems don’t necessarily have the same ability correlations as humans. AI systems can now ace the LSAT, but cannot yet automate the legal profession: the correlations break down.
Even so, I think the LSAT is a decent benchmark for AI systems, precisely because it means something for humans. It doesn’t seem too optimistic to hope that LSAT performance still checks one box in terms of what is required for doing legal work, even if we can’t infer that it checks as many other boxes for AI systems as it does for humans.1
On-the-Job Tests
It’s perfectly reasonable to ask, though, whether we can skip the correlations entirely. A great “so what” statement for a benchmark would be that, if an AI system does well on it, then the AI system is capable of automating a particular type of human labor. If we want an AI lawyer, why not design a benchmark to test legal work directly?
I think this is the right direction to go, and it will just take a lot of effort to get there. Human labor often takes place over a long time-horizon, involves interacting with many real-world systems (including other humans), and has difficult-to-specify success criteria. Researchers want to be able to run benchmark evaluations “in the lab”, and it isn’t clear how to operationalize this for such open-ended work.
I think the field basically acquiesces to the reality that economically-motivated businesses will try to use AI tools to improve their overall efficiency, and this may lead to automation eventually. But that’s little help for AI companies trying to figure out whether a new model iteration is something their customers will like.2 I assume the R&D teams at big AI companies do their best to create internal benchmarks that have some bearing on the question, but my guess is they’re at the beginning of this journey.
Still, there is some promising public work in the direction of seeing how well AI systems do when given complex human tasks with longer time horizons. For example, RE-Bench tests systems’ ability to do AI R&D itself. I haven’t evaluated this work in depth, but it’s the kind of thing you’d hope to see. One very worthwhile avenue, in my opinion, is simply to scale up that sort of benchmark: more complex tasks “in a box”. That is roughly the equivalent of an on-the-job performance evaluation, which anyone who has ever hired and managed people knows is far more informative than isolated tests, whether given in an interview process or an academic context.
That is probably the right direction, but it will take time to mature. In the meantime, I think there remains a role for narrower benchmarks more akin to academic exams.
Examining the Exam
Having laid that groundwork, we now come to this post’s specific critique of many current AI benchmarks, and Humanity’s Last Exam (HLE) in particular.
We’re talking now about benchmarks that were not designed for humans, and thus did not survive an evolutionary process of serving a useful purpose within some broader human endeavor. Above all, I think this means we have to proceed very carefully. We should have a very clear hypothesis of what the “so what” is for any such benchmark.
Compare, for instance, designing a benchmark around one of the following four sets of exam questions.
Exam questions given to PhD students in all disciplines
Exam questions given to PhD students in a single discipline
Exam questions given to PhD students in a single discipline, which are judged to have a particular degree of difficulty
Exam questions given to PhD students in a single discipline, which are judged to have a particular degree of difficulty for a particular reason
The draw of (1) is obvious: success means it’s “as smart as all PhDs” or something like that. But, because we know the correlations of ability break down, we can’t really expect that to be the right inference. That’s why I think the “difficult for a particular reason” part of (4) is so important. We can’t just say that the task is something humans do, we need to have some concept about what ability humans are using to do that task, and we need to hone the benchmark to test that ability specifically. In other words, if you think you want (1), I think what you really want is a lot of copies of (4).
The main thing I like about the FrontierMath benchmark, which I’ve written about, is that it is in the ballpark of (4). Even if I think the reasons for its questions’ difficulty might be a bit muddled, you can see how to get a handle on it.
Humanity’s Last Exam, on the other hand, is closer to (1). Not to put too fine a point on it: the questions in HLE are all over the place. I’ll spend the rest of this section backing that up with examples, then conclude by saying what I think a more helpful version might look like.
Delving In
From the HLE paper:
[HLE] is designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 2,700 questions across dozens of subjects, including mathematics, humanities, and the natural sciences.
Already this raises an eyebrow: 2700 isn’t that many across “dozens” of subjects. The HLE website even says “hundreds” instead of “dozens”. It would be one thing if this were acknowledged to be a coarse sample, but it’s another thing entirely to claim this is the last test of its kind.
Questions were written by nearly 1000 different authors, each a subject-matter expert in their field. Each question is either multiple-choice or short-answer. Some of the short-answer questions must be judged by LLMs, but the answers are meant to be simple enough that this doesn’t cause significant issues.
Before submission, each question is tested against state-of-the-art LLMs to verify its difficulty - questions are rejected if LLMs can answer them correctly.
Oh come on! This guarantees that it will look like current models can’t do well on the benchmark, but question authors could easily overfit to that. I speculated whether this was a subtle issue for OpenAI on FrontierMath, but it’s another thing to make it an issue by design.
Due to the advanced, specialized nature of many submissions, reviewers were not expected to verify the full accuracy of each provided solution rationale if it would take more than five minutes, instead focusing on whether the question aligns with guidelines.
They go on to say that they hope the community will help catch mistakes. But mistakes are the least concern: do we have any idea what it takes to solve these problems, and what it would mean if an AI system could do so?
Amongst the diversity of questions in the benchmark, HLE emphasizes world-class mathematics problems aimed at testing deep reasoning skills broadly applicable across multiple academic areas.
Math is at the center of the exam, which is a large part of why I’m covering it on this blog. In fact, 41% of HLE questions are math problems. So much the worse for the dozens/hundreds of other subjects! For now let’s just pretend it’s a math-only exam.
I sampled 10 questions at random from the 1061 questions in the “Math” category which didn’t include an image in their input.3 Here’s what I found, sorted roughly in ascending order of problem difficulty.
Euclidean Geometry
The easiest problem looked to me to be easier than the easiest AIME problem. Here it is, rephrased for clarity.
Inscribe a square in a circle. Then, inscribe a smaller square in one of the segments between the square and the circle. That is, one of the smaller square’s sides lies on one of the larger square’s sides, and the other two vertices of the smaller square lie on the circle. What is the ratio of the side lengths of the squares?
HLE includes an author ID, and this author has 11 problems in the dataset: about 1% of all the math problems. They all look to be geometry problems of comparable difficulty. This is part of what I mean by “all over the place”. When a model does well on HLE, is that because it is doing easy high school geometry, or something else? There’s nothing wrong with a benchmark for easy high school geometry, but it is less helpful to have a benchmark that has easy high school geometry mixed in, undifferentiated, with very different sorts of problems.
This would be easier to swallow if models were just getting this problem right out of the gate, but they’re not: the answer to this problem is wrong in the dataset. There is a “rationale” field in the data, so we can see the author’s solution, as well as their answer. In this case, the author just made a mistake. o3-mini-high actually gets it right, but would be marked as wrong given the answer key. (I submitted a bug report.) Worse, I looked at another one of this author’s problems, and, while the answer was right this time, there was a fatal typo in the problem statement rendering it geometrically nonsensical. I could only discern the original intent from the rationale. (I submitted another bug report.)
I don’t know how much to harp on these errors. Any benchmark will have some mistakes, but it doesn’t inspire confidence. Ostensibly this author was paid $500 per question to write questions that LLMs got wrong, and succeeded by writing nonsense. Correction: only the top 550 questions out of 3000, as judged by the organizers, were monetarily compensated.
K-Theory Lookup
The next-easiest problem, by my lights, was this:
I don’t know any K-theory, but here’s what the problem author says for the rationale:
This is Theorem 1.2 of arXiv:2409.20523 "Exact bounds for even vanishing of K∗(Z/pn)" by Achim Krause and Andrew Senger.
Let’s take a look…
In our problem, p=3, n=3, and we want the largest i such that 2 divides i and i≤6. So the answer is 6.
A concern with FrontierMath was that success might require only light mathematical reasoning if coupled with high levels of background knowledge. But at least it set the goal of avoiding this! HLE doesn’t seem to have made any such effort.
Just to check, o3-mini-high doesn’t get this question on its own, but does get it when tipped to consider this paper.
In other words, this is essentially a search problem. No K-theory required! Again, it’s fine for a benchmark to target such search problems, but much less helpful when the search problems are mixed in, undifferentiated, with very different sorts of problems.
A “Well-Known” Fact from the Theory of Modular Forms
This one has a similar flavor.
Again, I don’t know anything about this field, but the author rationale says,
It is well-known that the theory of modular forms gives a homeomorphism from X to S³ less the trefoil knot. The knot complement of the trefoil is well studied.
o3-mini-high doesn’t get this question on its own, but what if we just give it the “well-known” fact? Sure enough, when asked for the first homology group of the complement of the trefoil, o3-mini-high gets it right 4/4 times. Indeed, o3-mini-high says that it’s well-known that the answer is the same for any knot complement. This appears to be true, and is simpler than the author’s solution. So, again, we seem to have what is mostly a search problem.
Linear Algebra Homework?
I’m unsure how to score this one. I think the solution given in the dataset might be wrong, but I’m very rusty on linear algebra. There’s a step in the answer rationale that seems obviously wrong, though, and, for what it’s worth, o3-mini-high picks up on the same step as being in error. Furthermore, o3-mini-high makes what looks to me like a tight case that the answer is different from what’s stated in the dataset.
If anyone wants to solve for yourself, please do so! HLE has a $100 bug bounty, so it might be worth your while. See instructions for how to claim it in this thread, and the ID for the problem in this footnote.4
Either way, this problem is low-to-medium difficulty on an undergraduate linear algebra problem-set. By this point, you know the drill: fine to have a benchmark about undergraduate linear algebra; less helpful when it’s mixed in, undifferentiated, with easy Euclidean geometry, search problems in K-theory, etc.
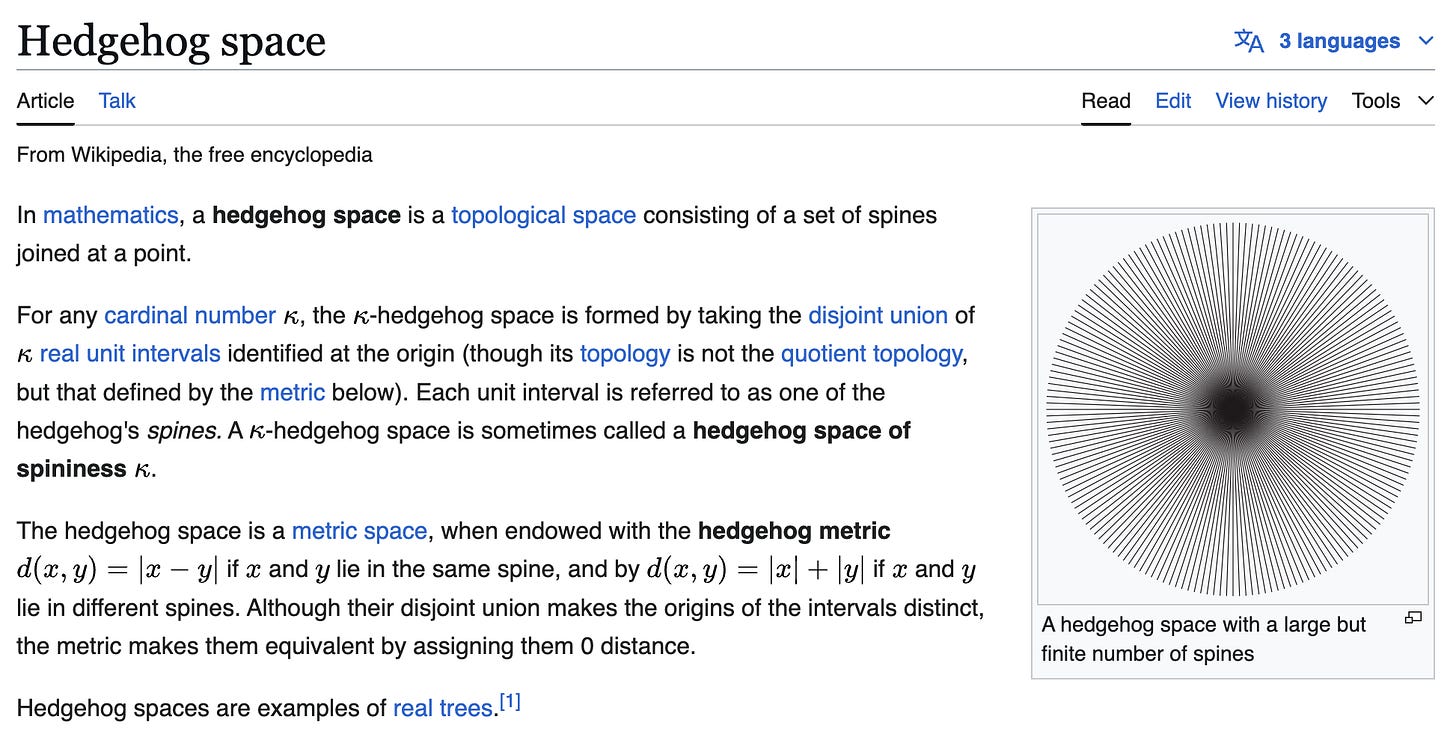
The Hedgehog Knows One Big Thing
There is an example of such a space, with arbitrary cardinality, that is well-known enough to have its own Wikipedia page.
I didn’t know this so it was fun to learn about. But, once again: search problem! I don’t know why o3-mini-high doesn’t get this right. It seems convinced that X is separable, and hence has cardinality no larger than that of the continuum. But, in any case, we’ve now added to our benchmark, “familiarity with well-known topological examples”. Fine, that’s a part of math! But we’re 5 questions into a 10 question sample and we’ve seen very little sophisticated mathematical reasoning.
Generating Functions
The author rationale explains that this is an exercise in composing generating functions, and that the answer is the coefficient of x^21/21! in the expansion of e^(1/(2 - e^x) - 1). He mentions that WolframAlpha can do the extraction.
It’s a bit of a digression, but I found o3-mini-high’s performance here pretty neat. When told to write a script to find the desired value, o3-mini-high wrote a correct script. However, the script didn’t finish in under a minute on my laptop. So, I said, “That doesn't finish running on my laptop. Can you be more efficient?“ and it gave me a script that got the right answer near-instantaneously. It didn’t even use the nice generating function that the author intended, doing this instead:
When I asked it for a more concise generating function, it gets the intended one.
Anyway, I would characterize this problem as similar in difficulty to an AIME problem, modulo the familiarity with generating functions. This is the most sophisticated mathematical reasoning we’ve seen so far, but I’m not sure it tells us much we didn’t already know from the AIME.
0s and 1s
Edited a bit for clarity:
Consider two sequences of binary digits, 0 and 1, each containing 100 digits. Call one the initial sequence and the other the target sequence.
An operation allows for either inserting one or more identical digits at any position within a sequence (including the beginning or end) or removing one or more consecutive identical digits.
What is the minimum number of operations, n, needed to guarantee the ability to transform the initial sequence into the target sequence?
I think I like this problem. It seems to require careful logical thinking and no particular background. The only issue is I don’t think the author’s rationale is adequate, so I’m not sure of the right answer. Transforming a sequence of all 0s into an alternating sequence 01…01 seems to require 51 operations. The author claims this is always sufficient. I’d love to see a proof, if anyone has one!
Unfortunately, this probably means the problem is pretty guessable: you get the lower bound and just go with it. That is, success won’t necessarily reflect deeper understanding. Although, for whatever reason, o3-mini-high seems incapable of answering 51: it’s really convinced 50 is enough.
The Homework Problem No One Got
This looks like a tricky problem indeed. How do I know? The author says it is from the homework of an algebraic number theory class at ETH Zurich, and “not a single student was able to solve the exercise”. The class looks to be either upper-level undergraduate or introductory graduate level, and ETH is known for their strong math program. Not bad for external validity!
There’s a concern about data contamination: solutions to problem sets were posted on the class website. Funny enough, the solutions to this one problem set were taken down — perhaps for this very reason — but they’re still available on the Internet Archive. I tend to think this concern is a bit overblown, but it’s worth noting.
Beyond Me
I’ll treat the final two questions similarly, so here they both are.
These questions also rely on advanced background knowledge, but, unlike the previous such examples, they don’t seem to be purely search problems. They don’t look super involved either, but I’m unfamiliar with the content so that’s just a guess.
The solution to the first problem seems to be applying some relatively straightforward facts about dimensional constraints on the relevant objects. E.g., “12 is the maximum rank, and A11 on its own already occupies the entire rank.”
The solution to the second problem appears to require some initial observations about the nature of the quotient stack, and then applies something called the Harer-Zagier formula, which it cites from a paper.
These strike me as comparable to easy-to-medium FrontierMath problems, though with the same concern about it being hard to tell how much background vs. creativity is required.
Tallying Up
In summary, we found:
1 easy geometry problem (answer is wrong)
3 search-ish problems, from moderate to advanced domains
1 straightforward linear algebra problem (answer might be wrong)
1 straightforward generating functions problem
1 discrete math problem, nice but guessable
1 challenging algebraic number theory problem (good external validity)
2 problems requiring high background and at least non-trivial execution
Suppose a system got 50% of the math problems on HLE correct. What would we make of that? I think, given this variety, we wouldn’t really know. It could reflect AIME-level problem-solving ability plus an improved search ability. That would be my guess, though it could be something else: it would depend on which 50%.
What if it got 90%? I think we would say this reflected some additional problem-solving ability beyond a score of 50%, but it would be hard to say anything more precise. I don’t think we’ve seen anything that would let us conclude, say, that such a system would be able to solve any short-form math problem that the 90th percentile of math grad students could solve.
Also, keep in mind these are only the math questions! There’s also philosophy, physics, literature, history, and biology in the full benchmark. If you see an aggregate statistic about HLE, how some model got 30% where the best previous model only got 10%, I think that is basically impossible to interpret.
Last Exam… v2
Maybe it’s just that the bombastic name of the benchmark rubbed me the wrong way. Or maybe it was the accompanying PR blitz, like this New York Times article titled, “When A.I. Passes This Test, Look Out”. (Look out for what??) So, fine, I admit I am picking on HLE in particular. Just a bit.
But, bombast aside, I think the work could be useful, if sufficiently elaborated. I think this would need to involve figuring out why the question authors think their questions are hard. From there, the test could be broken down not just by subject area, but by cognitive skill or task category. Even a benchmark composed entirely of “homework problems that advanced undergraduates in top math departments all got wrong” would be pretty interesting.
Regardless, the goal is to go beyond, “GPT-5 got a higher score on HLE” and get to something more meaningful, like, “GPT-5 scored perfectly on questions requiring applying theorems from research papers but still struggled with questions requiring combinatorial reasoning”. I think that would be a good step toward “so what”.
This isn’t guaranteed. It might be possible to make an AI system that was highly specialized to the LSAT, perhaps engineering it to exploit quirks in LSAT questions specifically. The more a system does this, the less it is likely to have general abilities.
Or whether it has become dangerous in some way.
An additional 45 questions included an image. I excluded these because I wanted to be able to try out o3-mini-high if that seemed like it would be informative, and o3-mini-high doesn’t process images.
66f684db71131a41ff244fb9



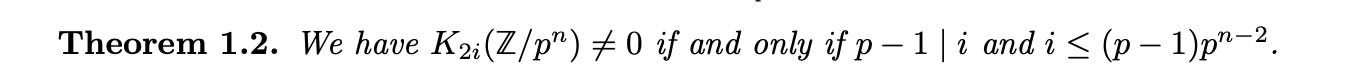








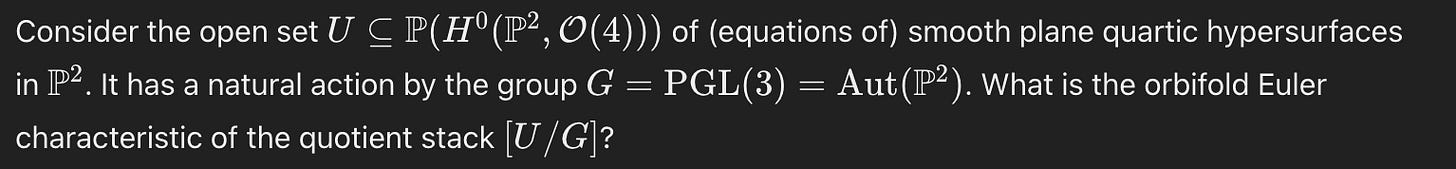
Great post! Really insightful breakdown.
"Maybe it’s just that the bombastic name of the benchmark rubbed me the wrong way."
I think a lot of people are with you on this. My own tiny gripe: if you're going to name something Humanity's Last Exam, don't have multiple choice questions. It turns whatever the problem was into a search problem, and potentially a very trivial one.