What Does It Mean That AI Is Now Good at the AIME Math Competition?
Delving into a popular benchmark
Update: the 2025 AIME I has since taken place. See this post for an in-depth look at how the best AI systems performed.
Setting the Stage
In September of last year, OpenAI announced that their new model, o1, got a very good score on the 2024 American Invitational Mathematics Examination (AIME).
What is the AIME, and what is a “very good” score?
The AIME is an annual US high school math competition. It’s a 3 hour test consisting of 15 math problems. Answers to problems are integers between 0 and 999, inclusive. The subject matter of the test is drawn from a pre-calculus high school math curriculum. It’s not advanced math, but the questions are much harder than what you’d find in a typical high school class or standardized test.
The AIME is the second stage in the funnel for selecting the six members of the US team at the International Mathematics Olympiad (IMO), which is the pinnacle of high school math competitions. That funnel starts with a test that’s open to any US student. The top ≈15% on that test are invited to take the AIME. The top ≈5% on the AIME, about 300 students, are invited to the third stage.
o1’s score on the 2024 AIME was high enough to get invited to that third stage. In other words, o1 scored in the top 0.15*0.05 = 99th percentile among those high school students who took the initial test, presumably already a self-selected group.
Why is this interesting?
o1 can thus do something that no prior AI model could do and that previously only very mathematically talented humans could do. I was into math in high school and my scores on the AIME were a bit above average at best. I remember it being hard. That alone was enough to pique my interest about o1’s performance.
All the more so because I find most AI benchmarks hard to situate. Results all sound like: the new generation of models does well on a test that was designed 6 months ago to stump the old generation of models. What are we supposed to make of that? Too often it feels disconnected from anything else.
The AIME is not that connected to the real world: it is contrived for humans by humans, not drawn from math problems naturally encountered when trying to do a job. But at least the AIME has a life outside of AI: it’s the sort of thing that humans are familiar with and have opinions about. We can hope to answer, at least for humans, what makes the AIME hard. From there, we can try to understand a bit more qualitatively what it is that AI systems are getting good at.
This seems worth doing. We’ve been in the situation of “computers are better than humans at math” before, and it has been significant. To give the obvious example: calculators long ago outstripped humans in their ability to solve arithmetic problems. That may have seemed like a party trick at first, but eventually that (quite limited!) capability drove a large part of the 20th century technological and industrial boom. The recent AI results show that the frontier of what math a computer can do has been pushed out further, and we can try to understand what this means for applications in the world.
Lastly, it’s just wild that a language-based system like o1 is any good at math at all. Back in the “ChatGPT moment” in late 2022, the excitement was around how linguistically flexible yet relatively coherent these language models had become. It was ironic that the hot new computers were bad at math of all things, but not particularly surprising: precision wasn’t their natural element. So it’s surprising now that the same systems are getting better at math. I probably wouldn’t have been above a 25% chance of “elite AIME performance by an LLM” happening in 2024, and yet here we are. All the more reason to look into it.
What about other models?
September 2024 feels like a long time ago in the world of AI. While no model did well on the AIME before o1, there have since been two notable developments.
First, OpenAI announced their next model, o3 (apparently “o2” ran into trademark issues with the British telecom company O2). o3 did even better on the 2024 AIME than o1, getting a 14/15. It also is said to do meaningfully better than o1 on another advanced math benchmark. Overall we’ll take the perspective that the systems are acing the AIME, with a quick look at one exception. When we then look a bit beyond the AIME, we’ll also evaluate the best publicly available version of o3, currently o3-mini-high.
Second, the company DeepSeek released a model called R1, which does about as well as o1 on the AIME. Indeed, DeepSeek has been pretty transparent that R1 is more or less a replication of o1. That wouldn’t be of interest to us except for one difference: DeepSeek shows much more detailed output from R1 than OpenAI shows from o1. In particular, we can see R1’s full chain of thought, as opposed to just a final summary of o1’s. Think of the chain of thought as the model’s scratch work: all the text it generates as it breaks down the problem, considers alternative approaches, critiques its own work, and so on. In this article, we’ll treat R1 roughly interchangeably with o1, and we will take advantage of being able to see R1’s chain of thought.
Are the models cheating?
These models are trained on large bodies of text. What if the AIME problems and solutions are somewhere in there? That could certainly tip the scales in the model’s favor.
OpenAI claims that o1 was created before the 2024 AIME questions were released at all, which would be a pretty good safeguard if so. We’ll just have to assume that remains substantially the case with o1 today as well as with R1. Even if the models are now contaminated, we can at least hope that the shape of their answers is similar to what they would have been initially. Anyway, the 2025 AIME will be available soon, so we can get a fresh evaluation.
What will we analyze in this essay?
In the first and longest section, I’ll analyze three AIME problems that I’ve selected to run the gamut in terms of difficulty as well as the mathematical reasoning required. For each problem I’ll discuss a human solution and an AI solution.
Then I’ll summarize what we’ve learned and characterize more abstractly the capabilities that AIME performance seems to require. I’ll even speculate a bit about what sort of real-world tasks this might mean the new models are capable of.
Finally, since this article is mostly about success on the AIME, I’ll look at an example of a harder math problem where the current systems still fall short. This will give us a sense of the new frontier.
TL;DR?
My biggest take-away is that the AIME is primarily a hard test for humans because it is closed-book and timed. The problems mostly require remembering relevant math facts and applying them in straightforward ways. If you try that enough, you’ll solve most AIME problems. The challenge for humans is not being able to look anything up and getting it all done within the time limit.
It’s very impressive that AI systems, especially language models, can do this at all. But it’s playing to a computer’s strengths of memory and speed in a straightforward way. Indeed, a human needs pretty good intuition to call up the right facts and apply them within the time limit. A computer doesn’t have to be so efficient.
Thus, I would characterize the frontier of AI math capabilities as having moved out to problems that require more creativity. I don’t see much evidence yet of that capability.
If you want to get a hands-on feel for AIME problems, for the first time or as a refresher, then read on! If you only want to read a bit more, skip to the AIME Conclusions section. If you want something in between, skim the Human Analysis and AI Analysis of each problem, and read the Take-Aways sections at the end of each.
AI on the AIME
The AIME’s 15 problems are ordered roughly by difficulty, so we’ll consider one from each third of the 2024 test, selected to cover diverse content areas. I’ll use the notation P* to denote a problem, e.g. P3 is the third problem.
P3
Human Analysis
If you haven’t seen this sort of problem before it might not be clear how to get started. Indeed, not knowing how to proceed is, in my experience, the gut feeling of what makes a problem hard.
Solution
At least in this case, though, there’s something sort of obvious to try: work out the answer for small values of n and see if a pattern emerges.
Alice takes 1 token: L for Bob.
Alice takes 1, then Bob takes 1: W for Bob.
Alice takes 1, then Bob takes 1, then Alice takes 1: L for Bob.
Alice takes 4: L for Bob.
If Alice takes 4, then Bob takes 1 and wins; if Alice takes 1, Bob takes 4 and wins: either way, W for Bob.
If we continue, we’ll get the first 10 L/W’s for Bob like so:
L
W
L
L
W
L
W
L
L
W
We might notice, then, that 6-10 repeat the pattern for 1-5. If that pattern holds indefinitely, we’re nearly done: for every group of 5 up to 2020 Bob will have two W’s for a total of 2*2020/5 = 808, and then in the final chunk of 2021, 2022, 2023, 2024 he’ll have one more W (2022), so the answer is 809 – and indeed that’s correct.
That might seem a bit unsatisfying, and sure enough there is a more conceptual way to solve the problem. First note that, so long as the pile has more than 5 tokens in it, Bob can always do the opposite of what Alice just did: if she takes 4, he can take 1; if she takes 1, he can take 4. Doing this guarantees that, after each of them has had a turn, the pile will have decreased in size by 5. Alice can play a version of this too: apart from her very first turn, she can mirror Bob as well, and the pile will decrease by 5 after each turn – plus whatever she took on her first move.
Having analyzed what happens in the cases of n=1, 2, 3, 4, and 5, we know that Bob loses if it’s Alice’s turn when the pile has 1, 3, or 4 tokens, and Bob wins if it’s Alice’s turn when the pile has 2 or 5 tokens. So, if the pile starts out with a multiple of 5 tokens (10, 15, 20, …) or 2 more than a multiple of 5 tokens (12, 17, 22, …) then Bob can play the “mirror Alice” strategy to decrease the pile by 5 each time, and eventually it will be Alice’s turn with either 2 or 5 tokens, and Bob will win. Similarly, if the pile starts out with 1, 3, or 4 more than a multiple of 5, Alice can use her first move to reduce the pile to having a multiple of 5 tokens, or 2 more than a multiple of 5 tokens, and then she plays a “mirror Bob” strategy to decrease the pile by 5 each time, and then eventually it will be Bob’s turn with with either 2 or 5 tokens, and Alice will win.
That derives the repeating pattern in groups of 5 from first principles, and you proceed as above to work out the answer of 809.
Take-Aways
It’s hard to spot this argument if you haven’t seen something similar before, but practice with math competitions will expose you to many problems like this. In fact, this problem is something you’d find in any introduction to a branch of math called combinatorial game theory. Experience with this sort of problem or that branch of math will make it clear how to approach the problem.
AI Analysis
Solution
First of all, both o1 and R1 get the right answer. Here’s R1’s summary. o1’s is similar.
It has spotted the right pattern and has used that to compute the right answer. It’s unclear, however, whether it pursued the “brute force” approach of just recognizing that the W/L results repeat in groups of 5, or whether it made something similar to the conceptual argument above. This is where it’s really handy to be able to look into R1’s chain of thought. Here are some highlights.
First, it recognizes the problem as being from combinatorial game theory.
It then proceeds to list out the small numbers, much like we did above. (Its Ws/Ls are reversed from ours because it’s calculating whether Alice wins.) These chains of thought are full of little moments of uncertainty and double-checking, like here where it says “Wait, but hold on. Let me confirm.” I don’t know on any deep level why it does this, but it is certainly relatable — especially for a human taking the AIME, where any little slip-up might cost you the problem.
R1 works out examples up to 20 and then tries to spot a pattern by seeing how far apart the L positions are from each other. From this it hypothesizes the right overall pattern.
It checks this on more examples, re-checks smaller examples, and then uses the pattern to calculate the correct answer.
It’s worth noting that OpenAI’s 4o model, which is o1’s predecessor, also gets the right answer here, though it writes some code to perform the final computation of 809. So, we’re not yet into the territory where the latest models have made advances over the prior state of the art.
Take-Aways
What I find most notable here is that R1 didn’t get into the conceptual argument, really at all. This isn’t necessarily a bad thing: it might have correctly intuited (so to speak) that this problem has a simple repeating answer. But we might start to wonder to what degree it’s capable of taking a more conceptual approach.
P8
The inradius of a triangle is the radius of the incircle, which is the unique circle inside a triangle that is internally tangent to all three edges of the triangle.
The bit about m/n being relatively prime positive integers and asking for m+n is just a format to make the answer come out as an integer. Recall that AIME answers are always integers between 0 and 999, inclusive. The AIME often uses formats like this to allow for problems whose answers don’t naturally come out as integers.
Human Analysis
If you’re rusty on geometry it may be hard to know how to proceed, but this is a common type of geometry problem. What we need to do is use the given information to set up an algebraic system of equations, and then solve that system to get the answer.
For the sake of brevity, I’ll keep the solution at a high level and then discuss the take-aways separately. If you are indeed rusty on geometry, don’t worry about following the details.
Solution
Our first equation comes from calculating the length of side BC two different ways, using the two rows of tangent circles.
Specifically,
Our second equation relates these variables, using similar triangles formed by connecting B to the centers of the leftmost and rightmost circles.
The diagram above gives z/1 = x/34. An analogous diagram at vertex C gives w/1 = y/34.
Combining and rearranging we have,
We can use this with our first equation to solve for z + w and BC. Namely,
and
Finally we get to the incircle. Let r denote its radius. As before, we form two pairs of similar triangles, one pair on the left and one pair on the right.
This gives us z/1 = a/r and w = b/r. Rearranging and combining with the value for z + w, we get
But a + b = BC, so we can plug that in. We get
Solving for r, this yields 192/5. Using the specified answer format we get 197, which is correct.
Take-Aways
This solution is presented with the benefit of hindsight. When first starting out, you might go down several dead ends before finding anything useful. Even information that turns out to be useful can look suspiciously unhelpful when you first find it. When I was solving this problem and computed BC = 45696/11 I had a bad feeling that this was too messy of a number to be useful, but it turned out to be on the right path. This is a frustrating but realistic aspect of solving math problems: intermediate steps aren’t always pretty, and sometimes the night is darkest before the dawn. It takes discipline not to get overwhelmed as you go and judgement to know whether to push forward or backtrack.
The above solution glossed over a number of geometry facts, including:
If two circles of equal radius are tangent to the same side of a given line, then the line connecting the centers of the circles is parallel to the given line.
If two circles are each tangent to the same two sides of a triangle, then centers of the circles and the vertex of the triangle where the two sides meet are collinear.
Two right triangles are similar if they share one other angle.
The ratios of corresponding sides of similar triangles are equal.
Being fluent with these facts is critical for solving many AIME problems. Forgetting a useful fact, or just not thinking to apply it, can make all the difference.
To me, this problem has a bit of a flavor of throwing things at the wall and seeing what sticks. Maybe there is a conceptual argument that would put you on exactly the right track, but I don’t really see it. What makes this a manageable problem is that the specific methods that do eventually work are not particularly obscure or creative. “See if you can connect salient points to make similar triangles” is one of the most common problem-solving techniques in geometry. So, you just keep trying to derive equations until you have enough to solve, or else, as is common on the AIME, you start to feel the time pressure and decide to move on.
AI Analysis
R1 got this problem wrong the first time I asked, and when I asked twice more it only got it right once. o1 got it right three times in a row. I wouldn’t infer much about the relative quality of the models from this, though it’s helpful to be able to compare R1’s chain of thought between a success and a failure.
Incidentally, isn’t it surprising that language models can solve geometry problems at all? Humans will draw pictures as they go, but the AI systems can’t do that. Can they “see” the diagrams, in their mind’s eye, so to speak? I go back and forth between “don’t be silly” and “who knows”. Anyway, as we saw, the key to this problem is translating from geometry to algebra, and then solving the algebra. Maybe that is a decent fit for language models.
Solution
Let’s consider R1’s correct answer first. o1’s correct answers are all similar. Where we used z and w, it uses trigonometric functions like 1/tan(β/2), but the algebra works out the same.
As before, the chain of thought is more interesting. What stuck out to me most is that it kept trying to “remember” standard formulas that would let it set up an equation in one shot. A subset of geometry facts are specific formulas, ranging from better-known ones like the law of cosines to less-well-known ones like Menelaus’s theorem. No such formula is relevant for this problem, but it’s certainly worth checking.
There are some standard formulas involving the inradius, and R1 considers those but also seems to have the (correct) intuition that they’re not going to be so helpful.
After not making much progress down that track, it tries another approach: imposing a coordinate system. There are some problems for which this is the exact right approach.
But after a while – in a way that is extremely relatable – it gets bogged down in equations and decides to try something else.
One thing that seems really important for its success is that it’s honest with itself when it has an idea that doesn’t pan out. For example, here’s a spot where it hypothesized an equation that doesn’t make sense. You can almost see the hallucination materializing. But then it tests out the equation and realizes it doesn’t seem right: the equation gives two different values for what should be a single quantity. So, rather than bull ahead, it moves on. I don’t know this behavior was instilled, but it seems important.
Around this point it starts to hit on the right path, though it’s still a bit messy in its thinking – which makes sense, it doesn’t know yet which part is wheat vs. chaff. But the final equation below is more-or-less the same as our first equation.
And sure enough, from here it works out the intermediate value of 1190/11.
It’s about halfway there. It now needs to involve the inradius, and it did this in a way I found surprising. Where we used similar triangles, it pulls up a formula I’d never seen explicitly before (highlighted below). This formula is easy to prove, but I wouldn’t have thought of it as something to apply out of the box. I guess either R1 saw this somewhere in its training or else just intuited it, much like we intuited the utility of looking at similar triangles. Maybe a linguistic system has to rely on this sort of move a bit more, whereas humans might just draw a picture.
It’s smooth sailing from here: it works out the length of BC from a previous equation, and then double- and triple-checks its work for the final answer. That seems perfectly warranted, since the arithmetic is so gnarly. Humans certainly mess up AIME questions at this step, especially under time pressure.
What about when it goes wrong? I looked closely at the longer of the two failure cases, where R1 spent 11 minutes on it before giving up with a low-confidence guess. More than anything, I was struck by how similar it was to the success case. It makes some progress, eventually finding BC and what we called x+y, though it takes a while to get there, getting bogged down in a dead-end coordinate system approach. Then it needs to connect that to the inradius. It recalls a formula for the inradius in terms of the triangle’s area and perimeter, and spends some fruitless cycles trying to find the perimeter: in fact there isn’t enough information given in the problem to do this.
It also tries some more obscure geometry facts, such as Descartes’ theorem. This isn’t a particularly hopeful path, which it correctly judges – but it shows what a deep repetoire of facts it has at its disposable.
Eventually it gives up with style. First, it deadpans “we’re going in circles here” – I really have no idea this as a joke, or if that’s even a coherent concept. Then it admits it’s stuck, and desperately invents a formula that it hopes might “often” be the answer. I don’t know what inspired this formula, but it isn’t correct.
R1 then works out this formula, acknowledges the answer doesn't look good, and submits it anyway. Who among us…
For completeness: 4o also gets this problem wrong, and doesn’t seem particularly close. It seems to misunderstand the problem setup, thinking there are multiple triangles, and then does a computation that I think is just nonsense. This underscores how different o1/R1 are at this sort of task.
Take-Aways
For P3 we noted that the AI systems didn’t seem to be engaging with a potential conceptual argument latent in the problem. For P8, I’d say there isn’t any conceptual argument to be engaged with: it’s just a matter of casting about for useful equations until you have enough to solve the problem, and then you have to grind out the solution. That is exactly what it looks like the AI systems are doing, and they are doing it well. They call up various formulae to see if any are relevant and they apply various standard techniques to see what they yield. When they get enough equations on the board, they correctly solve them. When they fail, it’s just that they didn’t quite get enough to work with – but that doesn’t feel like a deep limitation.
P13
This problem comes in two steps. Step one is to find the smallest prime p such that p^2 divides n^4+1 for some integer n. It might be the case that there are multiple such n for this p. Step two is to find the smallest such n. The problem statement calls this final answer m.
Human Analysis
Here more than the previous problems we’ll need to use some well-known math facts, this time from the branch of math called number theory. As with P8, if you’re not familiar with basic number theory, don’t worry about following the details.
Solution
For step one, we’ll need to apply Euler’s theorem. Tailored to our case, we get that if k is the smallest positive integer such that n^k ≡ 1 (mod p^2), then k divides p*(p-1). In this context, k is called the order of n mod p^2. Additionally, we need the fact that, for any divisor d of p*(p-1), there is guaranteed to be a solution to the equation n^d ≡ 1 (mod p^2), and, if d is even, n^(d/2) ≡ -1 (mod p^2).
We want to find the smallest p for which there is an n such that n^4 ≡ -1 (mod p^2). This means that n^8 ≡ 1 (mod p^2), so the order of n mod p^2 divides 8. Since n^4 ≡ -1 (mod p^2), the order of n can’t divide 4. So the order of n is 8, and thus 8 divides p*(p-1). The smallest prime p such that 8 divides p*(p-1) is 17, which is the answer to step one.
How do we find the smallest solution to n^4 +1 ≡ 0 (mod 17^2)? There are three paths.
First is brute force: evaluate all values of n from 0 up to 17^2 and take the smallest solution. We could do that with a computer, but the AIME doesn’t allow computers.
Second, we could use another number theory fact: Hensel’s lemma. This gives a way to derive solutions to an equation mod p^2 from a solution to the equation mod p. We’d solve the equation n^4 +1 ≡ 0 (mod 17), not so bad to do by hand, and then apply the lemma to each solution. This is the smoothest path, but Hensel’s lemma is a little obscure for the AIME: it’s not any more advanced than typical content, but it’s not included in the standard curriculum either.
Third is what we might call “ad hoc Hensel”. Any solution mod 17^2 must also be a solution mod 17, so we first find the solutions to n^4 +1 ≡ 0 (mod 17) and then work out corresponding solutions mod 17^2. We just do this less systematically than the algorithm given by Hensel’s lemma. This is probably what AIME contestants were “supposed” to do.
I’ll present the third approach. First, we try the values n = 0, ±1, ±2, …, ±8 by hand and find that the solutions to n^4 +1 ≡ 0 (mod 17) are ±2 and ±8. We consider those one at a time.
For n=2, we write n = 17j + 2. We want to solve for
where we have used the binomial theorem to expand (17j + 2)^4 and eliminated the terms divisible by 17^2.
We can cancel a factor of 17 from the equation as well as the modulus, thanks to a basic fact about modular arithmetic. We then just need to find j such that
The solution is j=9. Thus, for n ≡ 2 mod 17, the corresponding solution mod 17^2 is 9*17+2=155.
The only part there that maybe seemed “lucky” was how we were able to cancel the factor of 17. Actually this is guaranteed to happen (exercise for the reader, or ask an LLM). At any rate, if we try the same for n=-2, 8, -8 we find we can solve similarly. The resulting solutions are 134, 110, and 179. The smallest is thus 110, so that is our answer.
Take-Aways
The less familiar you are with number theory, the more the above solution might seem arcane and tortuous. But for someone familiar with the area, the solution could be boiled down to this:
First use Euler’s theorem and the order of n mod p^2 to find p.
Then use Hensel’s lemma to lift solutions from mod p to mod p^2.
That is still presented with the benefit of hindsight. You might have to go down several dead ends before you get there. But, like P8, the problem is amenable to trying things out until something sticks. Euler’s theorem and Hensel’s lemma might not be the only things you think to try, but once you try them you’re nearly done.
This is challenging in the context of the AIME where you’re on the clock and you can’t look things up. But the AI systems have a very different relationship with speed and memory, so perhaps we shouldn’t be surprised that they do well.
AI Analysis
As with P8, R1 only got this question one out of three times and o1 got it every time. Unlike P8, however, R1 was pretty close with both wrong answers. In both cases its mistake was in step 2, where it found one solution to n^4 +1 ≡ 0 (mod 17), correctly found the corresponding solution mod 17^2, but didn’t look for other solutions mod 17, and so wound up with the wrong answer.
Solution
Here’s R1’s correct answer. o1’s are similar, with small differences I’ll note below.
As before, the chain of thought is more interesting. R1’s right and wrong answers were so similar I’ll just analyze them in one shot. Here it is finding the order of n mod p^2.
I’m not sure why it decides to rule out p=2 explicitly. On the one hand, 2 is a weird prime and often it is an exception to theorems involving prime numbers. But I don’t see a reason why it needs to be checked here specifically. Either I’m missing something (very possible) or R1 is just doing that as an over-generalized habit. It doesn’t hurt.
For the most part, both o1 and R1 made use of Hensel’s lemma. However, once R1 kept recalling an incorrect version of the lemma, and had to resort to the ad hoc approach we took above. R1’s struggle is once again relatable: on closed-book tests like the AIME, it’s a bummer to suspect that there’s a useful fact but not quite be able to recall it. You then have no choice to work more from first principles, and that’s bad when you’re racing the clock. Luckily for R1, this wasn’t an obstacle.
Here is R1 recalling Hensel’s lemma correctly. Note the “not≡0” part. Incidentally, you can also see it begin to lose the thread at the end, where it’s only considering lifting a single solution. It doesn’t recover from that.
And here is R1 recalling Hensel’s lemma incorrectly: it’s missing the “not”. It seems to know something is wrong, as it keeps trying to recall it “correctly”.
Again this seems to be the sort of pattern that helps stop hallucinations, but it isn’t strong enough to get R1 to recall the correct form. Even so, it is able to pursue the ad hoc solution correctly.
o1’s more summarized output appears similar. The only variation I noticed was, once, o1 didn’t consider the order of n mod p, but rather checked by hand for solutions to n^4+1 ≡ 0 (mod p) until it found 2^4+1 ≡ 0 (mod 17). It then argued, using Hensel’s lemma, that this could be lifted to a solution mod 17^2 – so indeed p=17 was the answer for step 1.
This is valid, even a clever application of Hensel’s lemma, but it’s also a little brute force compared with the other solution, since it involves an exhaustive check of several dozen values for smaller p.
Again for completeness: 4o got this problem wrong four out of five times. The one time it got it right was by writing code to do a brute force search. When it tried to reason “by hand” it wasn’t particularly close. In one case it did try to reason about the order of n mod p^2, but it quickly went wrong from there. I was curious if it would at least reference Hensel’s lemma, but it never did.
Take-Aways
Overall I have a similar take on P13 as P8. The solution to P13 is, if anything, more structurally straightforward: there’s one set of facts you need to get step one, and another set of facts you need to get step two. If you can manage to recall the right facts and apply them in a straightforward manner, you get the right answer. When o1 and R1 are correct, that’s exactly what they’re doing. The one notable difference was the way in which R1 got the answer wrong. When it got P8 wrong, it was essentially failing to recall an important fact. When it got P13 wrong, it was essentially just failing to properly apply the facts it had recalled. If it were a human, we’d say it made a careless error on P13. Again, this doesn’t feel like a deep limitation.
What AIME Problems Does It Get Wrong?
There are a couple AIME questions o1 gets wrong, but I don’t find them so interesting.
Here’s the one that o3-mini-high also gets wrong, P12:
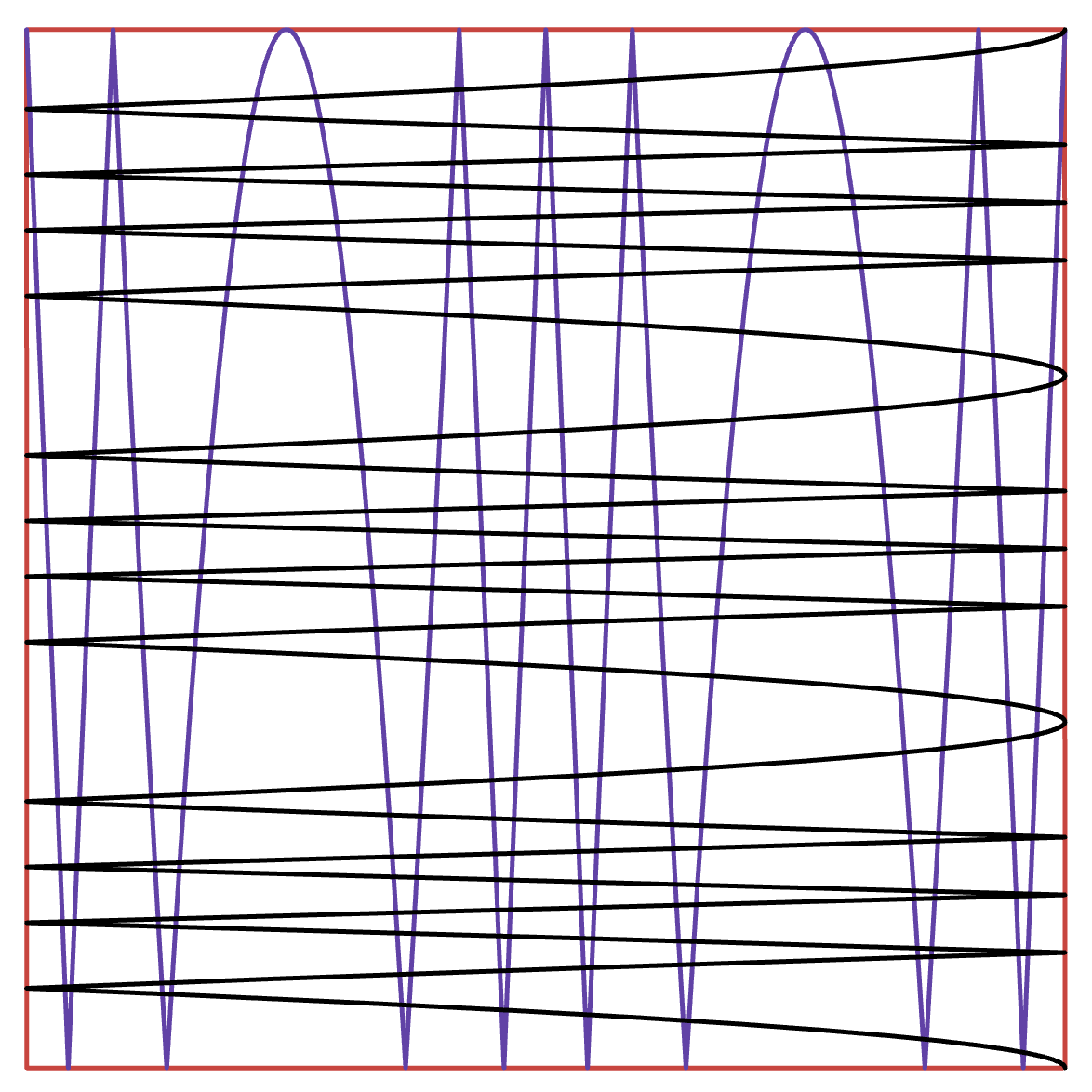
This problem is awful. You just have to work your way through the nested functions to get a sense of the shape of the graphs. Here’s what these graphs look like in the unit square, where all their intersections are, courtesy of an online graphing calculator.
There’s nothing interesting or insightful about doing this by hand: it just takes discipline. In the final tally you do have to be very careful around (1,1) as there are two intersections very close together, so it’s easy to miss one. But that’s the whole problem. Some AIME problems are like this: total slogs which no one should ever do by hand in real life. o1 gets some such problems but misses this one. I can’t blame it.
I’m being glib, but to justify that attitude let me point out that none of these models can do arbitrary-precision arithmetic “by hand”. Give them big enough numbers to multiply together and they will make a mistake. Knowing that limitation, a failure on this problem isn’t so surprising: it’s not so different from asking it to multiply two 20-digit numbers together.
AIME Conclusions
We want to know what it means about AI systems that they are good at the AIME. This is more a question about the AIME than it is about AI. What does it take to be good at the AIME? I chose the above three problems to give a taste but I’ve also analyzed many more and here’s my overall take.
Solving an AIME problem requires two main ingredients:
recalling the right facts and problem-solving techniques, and
applying those facts and techniques rigorously to get the right answer.
The relevant facts and techniques are generally well-known, and the process of applying them is conceptually straightforward though at times painstaking. The test requires knowledge and mental discipline, but it doesn’t particularly require conceptual insight or creativity.
I think what makes the AIME an especially hard test for humans is that it is closed-book and timed. Closed book because, while the relevant facts and techniques are all well-known, recalling them in the moment can be hard. Timed because, even though applying the facts and techniques is usually conceptually straightforward, it is hard to avoid careless errors under time pressure. I think an AIME that was open book and untimed would be far less differentiating among humans.
What does it mean that AI systems are good at the AIME? It means they are recalling the right facts and applying those facts rigorously. Looking at the chains of thought, this appears to be exactly what they’re doing. On one level this makes sense: when it comes to math, computers have always been good at memory and speed. Of course, that was the old generation of computers: language models do not, out of the box, recall facts correctly or apply them with rigor. So, the impressive progress is that language models are doing this at all, and the limitation is just that the test seems less inherently hard than we might initially think.
What does this mean about the tasks that an AIME-capable AI system can now do? We might look for cases where there is a standard battery of “facts and approaches” that need to be applied rigorously to individual cases, but still in a relatively straightforward manner. Perhaps we look for cases where human-devised policies and constraints have a mathematical or logical flavor. This could range from law to corporate policy to engineering. I admit that’s pretty vague! If I knew any answers with certainty, I’d be pitching businesses. I do wonder, though, if most practical cases still require a bit more out-of-the-box thinking than the AIME.
AI Beyond the AIME
The limitations described above are inherent to the AIME. Do they also represent the limits of these AI systems’ mathematical capabilities more generally? I’ll give one example that suggests this might be the case, and hope to follow up with more posts on the topic.
The AIME isn’t the hardest high school math competition: that would be the IMO. The IMO is given across two days, with 4.5 hours to solve 3 problems on each day. The problems are generally ordered by difficulty. According to this guide, the second problem each day tends to be a bit harder than the hardest AIME problem. Unfortunately for AI evaluation, the answers to IMO problems are proofs, which experts grade by hand. Sometimes, though, problems have simple numerical answers, which contestants must both find and prove to be correct. On these it’s at least easy to tell if an AI system got the numerical answer wrong.
One such problem is the second problem on the second day of the 2024 IMO.
In other words, there are 2022 monsters in a 2022-row-by-2023-column grid, one monster per row. Thus, there’s one “safe” column, though we don’t know which one to begin with. There are two other “safe” rows, the first and last, for a total of 2024 rows. Turbo has to get from the first row to the last row, moving left-right or up-down one step at a time. He has to start over every time he steps on a monster, but then gets to remember there is a monster there. How many tries does he need to guarantee he can get to the last row?
Obviously 2023 tries is enough: just try each column until you find the “safe” column, which, by bad luck, could be the last one you try. Can you do better? Maybe, maybe not! There are all sorts of ways you could try to be clever, but maybe they don’t work in general. This is where a proof comes in: whatever you claim the answer is, you have to prove it.
The neat thing about this problem is it requires no special math facts. Nor does it have the feel of a common sort of problem found in a specific branch of math. The solution is even relatively brief! It just takes creativity to find. Sure enough, no model gets the right answer today, and they don’t seem particularly close. But, to humans, this problem is only a bit harder than the hardest AIME problems. I won’t spoil it now, but if you want a solution I liked the write-up on page 12 here.
I have no basis for speculating on how long this sort of problem will remain beyond the capabilities of AI systems, but I think it represents an interesting salient in the current frontier: less about applying known facts and grinding through, and more about coming up with creative, conceptual arguments. That’s what I find fun about math, anyway, and at least for the moment it remains a human skill.