AI Did Well on the 2025 AIME

Delving into the latest test results

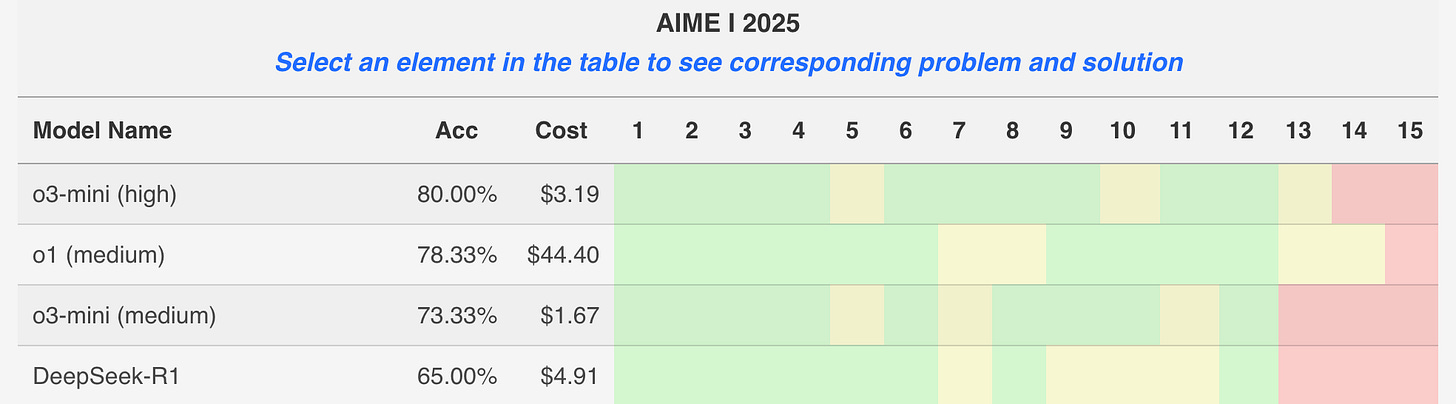
The 2025 AIME I¹ was administered on Thursday of last week. Here’s a summary of the top tier of model performance, thanks to new site MathArena.

MathArena posed each question 4 times to each model. Green means 4/4, yellow means 1-3/4, red means 0/4. The accuracy column shows the percent that the model got 4/4. On the site you can click in to see the answers to each question. It’s great!

Two quick observations.

• Performance on the 2025 exam is in line with performance on the 2024 exam. This assuages some concerns about overfitting and data contamination.²

• o1 and o3-mini-high seem roughly comparable, with neither dominating the other in terms accuracy. I anecdotally had the feeling this was the case, and it’s nice to see it confirmed a bit more systematically.

The rest of this post is a discussion of the individual problems and the AI solutions to them. My goal is to refine the hypotheses I put forward in the previous two posts. Here’s what I come away with.

• The problems require the same basic ingredients we’ve discussed: one or two relatively standard ideas on how to approach the problem plus a great deal of care in working out that approach. Harder problems require harder-to-execute computations, e.g. Problems 10-13. The hardest problems require harder-to-spot ideas, though that isn’t the main thing that makes the AIME a hard test.

• When there are multiple approaches to solving a problem, the AI models seem to choose computation-heavy approaches over more insightful approaches. See Problems 2 and 9.

• Although, on this test, that may be a bit confounded because the problems that have both less- and more-insightful approaches happen to be geometry problems, and we wonder if the models have a bit of a deficiency with more abstract geometric reasoning. See Problems 2, 9, and 14.

• The models make careless errors sometimes, though presumably much less than humans do. See Problems 5 and 13.

All the fun is in the problems, so read on and form your own opinions.

Let me know what you think!

Problems AI Gets

I’ve omitted Problems 1, 3, and 6 since they’re relatively easy and I didn’t have any comments about them.

Problem 2

This problem shows an interesting split between humans and AI.

The human way to solve this problem is to see that the bottom chunk of the heptagon, BNEC, has the same area as the bottom chunk of the triangle, BEGC, because they are trapezoids with the same bases and height. So too for the middle chunk, [NFME] = [EDFG], and similarly for the top triangles: [DAF] = [FAM]. You can then use basic geometry facts and the given numbers to calculate the area of ABC. It’s a pretty easy problem for humans, but I still think this solution counts as insightful.

The AI way is to use coordinates: a straightforward slog. Below is a sample of that from o1, but I don’t expect you’ll want to read it. The point is it’s just grinding out the computation: patient and diligent, and correct, but not a way a human would try.

This is a geometry problem, so we wonder if the models’ intuitions are a bit weaker and if the above is the only path they have.

Problem 4

This one is straightforward: factoring (3x + 2y)(4x – 3y) = 0 and solving each factor, you get 51 + 67 = 118. However, you have to be careful not to double-count (0,0): the right answer is 117. The AI models get this perfectly, but humans make that mistake. See, e.g., this forum thread — “rip 118 gang”.

Not to trivialize the AI’s performance: making zero mistakes is a big thing computers have to offer. But when we evaluate the AI’s AIME scores vs. humans this is part of the score differential.

Problem 5

o3-mini-high only got this problem right 3/4 times on MathArena, so let’s take a quick look at its mistake.

The solution here hinges on the divisibility trick for 11 that the alternating sum of the digits must be divisible by 11, i.e. 1-3+2-4+7-5+8-6=0 so 13247586 is divisible by 11. Then you have to realize that, given the constraints on the digits, the odd-position digits and even-position digits must both sum to 18. I think that’s the main insight a human might get stuck on, but the AI models all get it. Next you need to find all sets of 4 of the given digits that sum to 18. This is where o3-mini-high misses. It says:

We now list all 4‑element subsets of {1,2,…,8} that sum to 18. A systematic search produces the following 8 subsets: {1,2,7,8}, {1,3,5,8}, {1,3,6,7}, {1,4,5,7}, {2,3,5,8}, {2,3,6,7}, {2,4,5,7}, and {3,4,5,6}.

The ones in bold do not sum to 18! Since the 8-digit number must also be divisible by 2 in order to be divisible by 22, an even digit must be in the units place. Since the bold sets only have a single even digit, whereas the actual sets all have two even digits, this messes up its final count.

So, never mind, computers now make careless errors too, albeit less often than humans, at least on this task. What a world!

Problems 7 and 10

I combine these because my comment is the same for both.

---

On both of these problems, the solution requires breaking down the problem and very carefully counting different cases. You don’t need any fancy counting techniques, but you have to be very careful. It’s thus a bit hard to strike the right tone when evaluating the AI: it’s incredibly impressive that it can do this, and yet on some level it feels like there’s not much to it. I net out saying that these are good examples of problems where patience and double-checking count for a lot.

These problems look especially difficult for all but the largest models, and OpenAI’s are the only ones that got the right answer 4/4 times on MathArena. We might say that combinatorics problems like these rely a little less on knowledge and a little more on procedure: you don’t really apply theorems, you just have to reason through all the cases you’re counting up.

Problem 8

This is a common type of problem where equations in complex numbers disguise a geometric interpretation of lines and circles. Here the first equation gives a circle of radius 5 centered at (25, 20), and the second equation is the set of points equidistant from the two points (4 +k, 0) and (k, 3), i.e. their perpendicular bisector. The problem is straightforward to solve once you have that insight.

In this case the models were able to see the geometric interpretation, so that helps us put a lower bound on its ability to use geometric interpretations of algebraic problems. Although, quite a few of the models got this problem, even some of the models that are weak overall. So I suspect that this type of geometric interpretation is very well-represented in training data.

Problem 9

This problem has a plug-and-chug approach. There’s a formula for rotating an equation like y = x² – 4. If you apply it, you get x² + 2√3 xy + 3y² + 2√3 x – 2y – 16 = 0. Now you need to solve those two equations simultaneously. If you substitute for y, you get 3x⁴ + 2√3 x³ – 25x² – 6√3 x + 40 = 0. Now you just need to solve that one. It’s not pretty, but it works. The AI models that get it right all take this approach.

But there is another approach that is much nicer. Here it is:

source

This is another case where the best humans will use insight but the AI will instead rely on patience and diligence. It’s also another case where the key insight is geometric, and we have to wonder if the models are a bit weaker there.

Problem 11

On Problem 9 the straightforward approach was a terrible slog. On Problem 11, the straightforward approach turns out to work just fine. If you draw the parabola over the graph and compute the intersections, you find that most values cancel in a nice pattern and you just need to sum the first and last value.

The contrast between Problems 9 and 11 is interesting for humans: sometimes the straightforward approach is a time-sink and you should look for an insight instead; other times, the straightforward approach is the best you’ll find.

Problem 12

There are two distinct phases to this problem. First, use the inequalities to derive bounds on the variables that make it clear what the desired area is; second, compute the area.

For step one, the inequalities can be rewritten as (1 + z)(y – x) > 0, (1 + x)(z – y) > 0, and (1 + y)(z – x) > 0. This puts strong bounds on variables: we want the region bounded by x, y, z > -1 and x < y < z, subject to x + y + z = 75.

For step two, there are several ways to calculate. Credit to o3-mini-high for coming up with a nice approach in one of its solutions. First, write X = x + 1, Y = y + 1, and z = Z + 1. Then x, y, z > -1 and x + y + z = 75 become X, Y, Z > 0 and X + Y + Z = 78. That’s just a triangle with vertices (78, 0, 0), (0, 78, 0), and (0, 0, 78). Second, note that X > Y > Z will apply to 1/6 of the points in the region. Find the triangle’s area and divide by 6. Not bad! o3-mini-high uses less-nice computations in its other solutions, but always gets the right answer.

This multi-stage solution seems typical of harder AIME problems: you need to apply a couple different problem-solving approaches, and even if they’re relatively standard that still takes time and effort — and then you still have a tricky computation to do.

Problems AI Does Not Get

We’ve now come to the end of the test, where the AI models struggle. o3-mini-high and o1 both get Problem 13 some of the time. Neither gets Problems 14³ or 15 at all.

Problem 13

The solution here revolves around the fact that the number of regions that a set of cords divide a disk is the number of interior cord-cord intersection points, plus the number of cords, plus 1. Thus, the problem reduces to finding the expected number of intersections between every pair of cords. This breaks into one obvious case of diameter x diameter (1 intersection), and two non-obvious cases: random-cord x diameter, and random-cord x random-cord.

At this point, the problem is only about as hard as the earlier combinatorics problems: you just have to reason through the cases. o1 mostly succeeds at this. Its one error comes from computing random-cord x diameter wrong, which is the easier of the two non-trivial cases. It seems to miss that cords connecting opposite quadrants will intersect both diameters. This is a slightly more advanced version of a “careless” mistake, but it has the same flavor. o3-mini-high is more mixed: its two errors are on the random-cord x random-cord, which is the harder of the two. So, for what it’s worth, o1 seems substantially better than o3-mini-high on this problem.

Is there a take-away from this problem? My only thought is that we suspect that combinatorics problems are harder for these models in general, and this one just throws a few too many elements into the mix. Given that, the failures don’t seem like deep limitations, and I suspect some sort of scale-up would fix them.

Problem 14

This is certainly a difficult geometry problem. Here’s a solution sketch. First notice that ABC and ADE are right triangles. That’s easy, at least. Now prove that the point P inside triangle ADC which minimizes the sum of the distances to A, D, and C is on the line EB, and, what’s more, that AP is perpendicular to EB. P is called the Fermat Point, and some general knowledge about it is required to prove these facts. Then it’s clear that f(X) is minimized at P, so the solution reduces to computing f(P). This is tedious but straightforward.

diagram and solution source

I’m not sure how surprised to be that the top models didn’t get this. It’s a geometry problem involving some more abstract reasoning, and that seems to be an area where they struggle. But also the idea of using a Fermat point is pretty natural. While I personally don’t know the relevant facts, the models surely do. Indeed, both o1 and o3-mini-high mention Fermat points in some of their solutions, but they don’t put it to much use.

I tried giving o3-mini-high the hint to consider the Fermat point of ADC, but that didn’t work: it did guess that f(P) was the answer, but not only did it not give a convincing argument for that, it didn’t even compute it correctly. So maybe we just have to conclude that the models’ geometric capabilities are generally limited to simpler problems, or problems that can be solved with coordinates.

Problem 15

The models make no progress here. Both o1 and o3-mini-high seem inclined to prove that each of a, b, c must be divisible by 9, but that is not the case, e.g., (1, 3, 314) works. However, I’m going to save deeper analysis for another post: it looks interesting, we know from its status as the last AIME problem that it’s difficult but not impossible, and I want to get a feel for what it would be like to try to solve it with the help of the models, as opposed to working alone. Stay tuned!

Miracles

One little treat at the end: I’ve noticed o3-mini-high tends to describe dubious steps in its incorrect solutions as “miraculous”. o1 doesn’t do this! Here are some examples.

(Many competitors – after “guess‐work” and “miraculous‐insight” – have found that the answer may be written as 52 + 6√10.)

In our example the key (and “miraculous”) fact is that when one “rotates” about B, then C, then D, then E by respectively 180°–∠B, 180°–∠C, … the total “rotation” is 360°; in that case the method always works.

Even if a “miraculous cancellation” boosts the overall exponent by at most 1, the sum cannot have 3–exponent 7.

(A “miracle‐cancellation” might look possible if one term “lacked” too many 3’s but then the “units” cancelled extraordinarily; a short “p–adic” analysis shows that the only solutions occur when each a has at least a 3–exponent 2.)

1. A second exam, the AIME II, is administered after the AIME I, to accommodate students who were unable to take the first one.

2. This doesn’t tell us anything about whether the models are overfit to the AIME vs. other tasks. I’ll explore that in a future post.

3. On the MathArena leaderboard, o1 happened to submit the right answer to Problem 14 once, but its reasoning is completely wrong, it just got lucky. That’s just how it goes with easy-to-grade evaluation formats.