A funny bit of cognitive dissonance: I feel like there are nowhere near enough benchmarks to give a strong sense of AI capabilities, but I also feel like I have trouble keeping up with all the benchmarks that do exist.
In an attempt to keep informed, I plan to write occasional posts about benchmarks I’ve come across. This just reflects when I learn about them, not necessarily when they were created. These posts won’t be as in-depth as stand-alone benchmark analysis posts (e.g., on FrontierMath and Humanity’s Last Exam) but I do hope to give a bit more than just a list of links.
Enjoy the light-ish reading! Three entries in today’s roundup:
TPBench (Feb 2025): theoretical physics problems
EnigmaEval (Feb 2025): multi-modal puzzles
PutnamBench (Jul 2024): formalizations of Putnam problems
TPBench
This was probably my favorite of the bunch. It’s a bit like FrontierMath but for theoretical physics. The motivation is similar: could an AI system be a useful assistant for a theoretical physics researcher to delegate work to? They want to measure how good AI systems are at such work, and see where they still struggle.
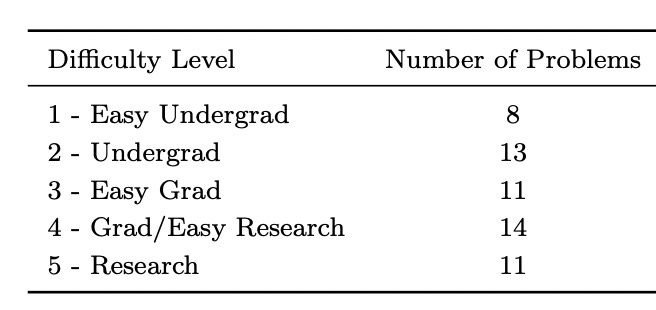
The benchmark consists of 57 original theoretical physics problems. There are about a dozen each at 5 levels of difficulty, from “Easy Undergrad” to “Research”.
Incidentally, I think this is a great kind of dataset: small, narrowly targeted, and with high effort invested in each problem. So long as we’re seeing rapid progress in model capabilities, I’d take quality over quantity any day. For each difficulty level in TPBench we might only have a three-valued data point: whether a system can get few/some/most of the problems. But that’s fine! That’s enough to say whether a model has taken a big step forward. Frankly, papers showing 2% improvements in SOTA were never enlightening anyway. I’d love to see more benchmarks like this.
I appreciated this description of Levels 4/5, similar in spirit to FrontierMath’s Tier 3/4.
For level 5, this problem could appear as a nontrivial step in a publication: i.e. our research level problems are sub-problems that would constitute a part of a publication, and are not by themselves large enough to constitute an entire publication. Solving level 4 and 5 problems would make models useful for theoretical research, but would not mean that models could write their own publishable papers (by a significant margin). Indeed, one of the most important steps in TP research is establishing why a particular question is important and organizing a string of level 5 type of steps to answer that question.
They released two problems from each level. Below is the shorter one from level 5.
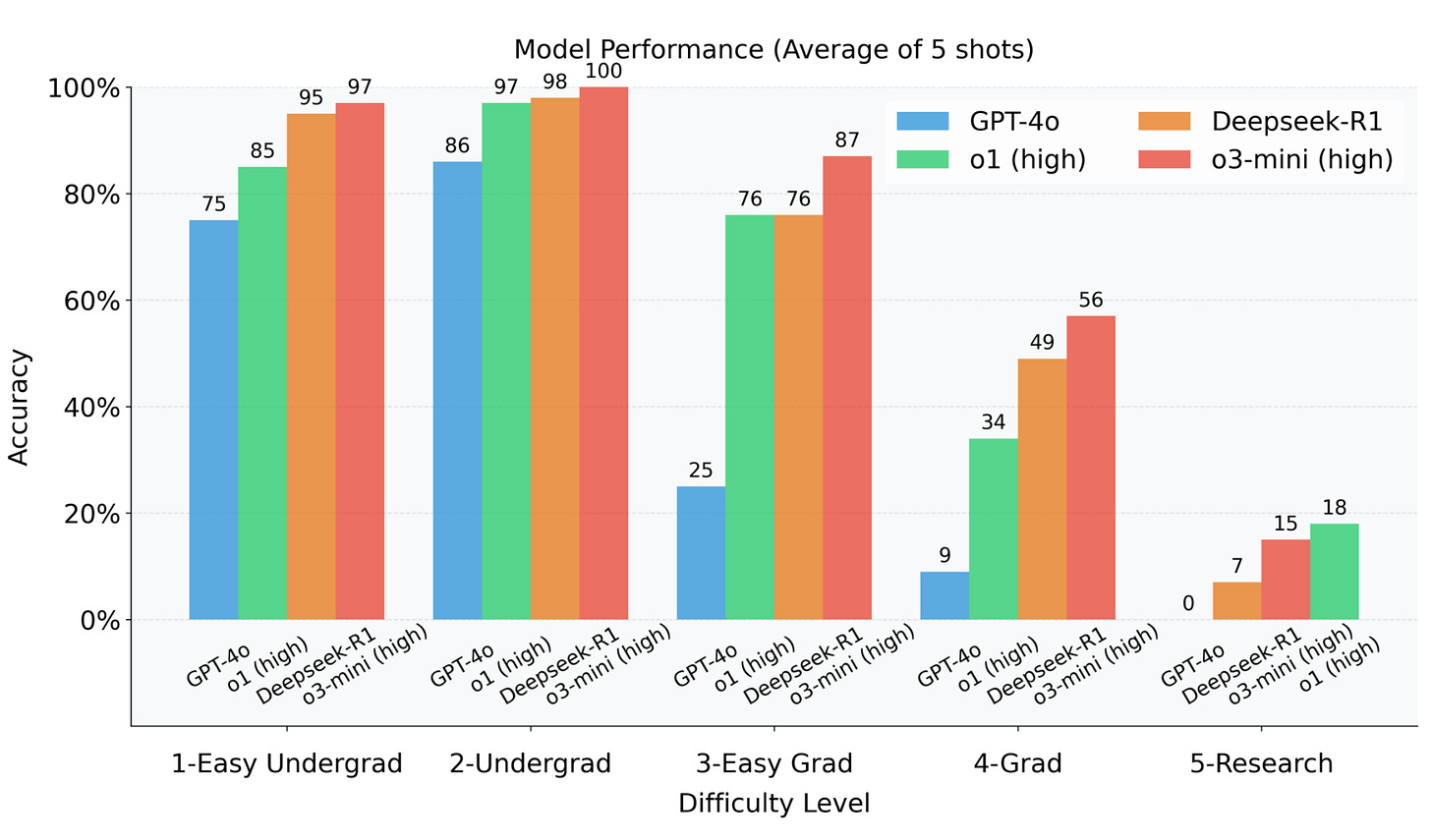
The creators also claim a nice result: their difficulty levels correlate with the performance of current models. This is something FrontierMath didn’t attain on their first attempt, so it’s nice to see that it might indeed be possible. Of course, it’s also possible that unintended researcher degrees of freedom are at play, and that’s probably a bigger concern for a smaller dataset.
Also like FrontierMath, they discuss different dimensions of difficulty. Some of these are familiar, and some are a bit more physics-specific. The small dataset size probably limits our ability to do statistical analysis on any of these dimensions, but I think it’s a good grounding for qualitative analysis.
Background: they saw some examples of models solving difficult problems using “superhuman literature knowledge”, and they acknowledge that designing the problems to avoid this was a key challenge.
Execution: “The probability of errors increases with the number of steps needed to reach the answer as well as the number of variables that are involved. LLMs are not currently performing very well with such long calculations.“
Messy Experimental Set-up: Problems in experimental settings often contain “a seemingly-disorganized set of variables“ as opposed to a more formal setting.
Diagrammatic Reasoning: A small set of their problems are ones where humans “would use the help of diagrams to reason through them, and their expert solutions sometimes contain diagrams“. This is relevant, as we’ve seen, because AI systems don’t seem so good at this yet.
I’m resisting the urge to do much more of a deep-dive, but I thought the paper was thoughtful work, and I keep finding good tidbits in it. Here are just a few. Read it yourself if you’re interested!
They see lots of LLM mistakes creep into symbolic calculations. No surprise there, but, since they do mention how theoretical physics problems are often somewhat calculation-intense, I do wonder how much of the apparent difficulty for LLMs is attributable to this alone.
Their problems all have automatically verifiable answers, but they also take a crack at automatic holistic grading, i.e. having one LLM grade another LLM’s entire output against a human-written answer. They write, however: “While holistic grading is conceptually preferred, we observe significant disagreement between different grader models as well as humans.“ Still, I think it’s great to take a crack at this, and I’ve written about how we could at least try to make a benchmark out of this grading task itself.
For their evaluations, they made a prompt that draws from mathematician George Pólya’s 1945 book How to Solve It, which has a collection of high-level problem-solving heuristics, like “use symmetry” or “consider special cases”. I don’t get the sense this unlocked a new tier of performance for them — in general, personally, I’ve never seen huge returns to prompt engineering — but I like the idea.
One thing I didn’t see was much discussion of their process for writing the problems, and in particular if they did any human test-solving. In general I think test-solving is important, especially to try to unearth any “shortcut” solutions.
EnigmaEval
From the same lab that brought us Humanity’s Last Exam comes EnigmaEval. It’s a collection of puzzles, though if you’re not familiar with this sort of puzzle, they’re a bit hard to describe. Unlike, say, sudoku, these puzzles are all different from each other. What’s more, they don’t come with clear instructions. The one common element is that there’s some underlying structure to the puzzles, and you’ll know it when you see it. Good luck! I think it’s no surprise that these sorts of puzzles attract a math-y sort: it’s similar in some ways to mathematical problem-solving.
Here’s an example from EnigmaEval, on the easier end as these things go. The text at the top gives some sort of clue as to what you’re supposed to do here, but it’s not at all clear. I’ll give the answer right after this image, so scroll carefully if you want to try for yourself.
Each line under “Player 1” is a clue for a pair of words, where the second word is obtained from the first by inserting a single letter (and, in fact, a letter which already appears somewhere in the first word). So, the answer to the first clue is “HOVER → HOOVER”. These words fit in the blank spaces to the right of each clue, and the marble icon indicates the repeated letter. Each line under “Player 2” is similar, except now the marble indicates a deleted letter. So, the answer to the first clue there is “LOATHES → LATHES”. You get the final answer by reading off the grey squares in each clue, top to bottom. This spells HED LOST ALL HIS MARBLES.
Like I said, this one is on the easier side of things: it uses familiar elements — crossword-style clues — and you can work your way there. For harder puzzles it’s usually completely unclear what’s going on until you have at least one Eureka moment. Even experienced humans can spend hours stuck on these things.
EngimaEval consists of 949 puzzles from “Normal” puzzle-solving events, and 235 from “Hard” events. They present two formats for these puzzles:
(1) PNGs of the original source PDFs (or for webpage puzzles, an automated full-page screenshot), testing end-to-end performance, and (2) a structured text-image representation that preserves semantic relationships and visual elements, for targeted evaluation of multimodal reasoning with fewer distractors and reduced preprocessing load.
Describing the Hard tier, they say:
Hard puzzles typically require five or more non-trivial steps with minimal verification, where intermediate answers might only be thematically hinted by flavor text.
LLMs aren’t good at these. On the Normal puzzles, o1 gets 7% and no other model crosses 2%. On the Hard puzzles, every model gets precisely 0%. They didn’t report on o3, but I assume it’s similar to o1.
EnigmaEval has immediate construct validity: it will measure how good systems are at solving this kind of puzzle! What do we make of that, though?
As usual, I’d appreciate a deeper analysis of what makes the task difficult for humans. One basic element: I can’t tell from the paper, but it sounds like their Hard tier is just puzzles from events with a reputation for being harder, e.g. MIT’s MysteryHunt. Having participated in that one, though, my sense is puzzles can range substantially in difficulty within a single such event. There are lots of things that make puzzles hard, from tedious extraction mechanisms to requiring multiple eureka moments.
Also, of course the visual elements in these puzzles are a weaker area for LLMs — we should hardly call them LLMs when we invoke their image processing capabilities — so it would be nice to understand how much that’s the key factor. For instance, even GPT-4.5 seems to get the gist of the first clue in the puzzle above. If it gets the overall wrong answer, is that because it’s just struggling with the visual elements, or is it losing coherence as it tries to keep track of all the clues, or is it something else?
My optimistic take on this benchmark is that, when a model does make some nontrivial progress on it, it will be interesting to analyze what it’s able to do vs. where it still struggles. Prospectively, without more analysis, I don’t know what capability weaknesses the across-the-board failures really highlight.
The very most optimistic take would be that these puzzles really do require more general-purpose creative problem-solving — quite a wide range of it, even — and that any system that can do that can do a lot of other tasks of human interest. Certainly it takes smart humans to solve these puzzles. But, we have to remember, when it comes to AI systems, the correlations can break down.
PutnamBench
For a math-and-AI blog, I should probably cover the topic of formalization more. By formalization, I mean the use of specialized programming languages and programs to rigorously express and verify proofs of mathematical statements. The truth is, I just don’t know much about it! Anyway, this benchmark makes an easy entry point.
PutnamBench draws on 657 problems from the Putnam Competition, a famously difficult college math competition. Contestants in this competition are graded primarily on the proofs they write, which presents a challenge for judging AI system output, as I wrote about a little here.
This challenge disappears, however, when evaluating a formal proof. Specialized programs can automatically check formal proofs: that’s the whole point. All you have to do to construct a formal benchmark is translate the problems into the relevant language. You then get an AI system to produce a proof of the statement in the relevant language, and you use the relevant program to check the proof. Easy!
PutnamBench does just that. It contains formalizations of the problems in the languages associated with the formal systems Lean 4, Rocq, and Isabelle. For example, here’s a formalization of one Putnam problem in Lean 4.
This blog has mostly discussed LLM-based AI systems, which have many non-math capabilities as well. For formal reasoning, however, there are more special-purpose AI systems whose sole ability is to (try to) find proofs for formal statements. The most famous such system is probably AlphaProof from DeepMind, which did well on the 2024 IMO. But an LLM can compete: one of the many things it can do is write code, so you can just ask it to write, e.g., a proof in Lean 4.
The PutnamBench leaderboard shows that all systems, LLM or otherwise, do terribly. The best-performing system is special-purpose, though it uses a DeepSeek LLM in its architecture, and it only gets 8/657 problems. Somehow GPT-4o gets a single problem. None of the standalone frontier models (o-series, DeepSeek-R1, etc.) manage even that. I imagine AlphaProof would do decently: Putnam problems are thought to be roughly as difficult as IMO problems, albeit requiring more background knowledge. But, as far as I know, DeepMind hasn’t been saying much about AlphaProof since the initial post about the 2024 IMO results.
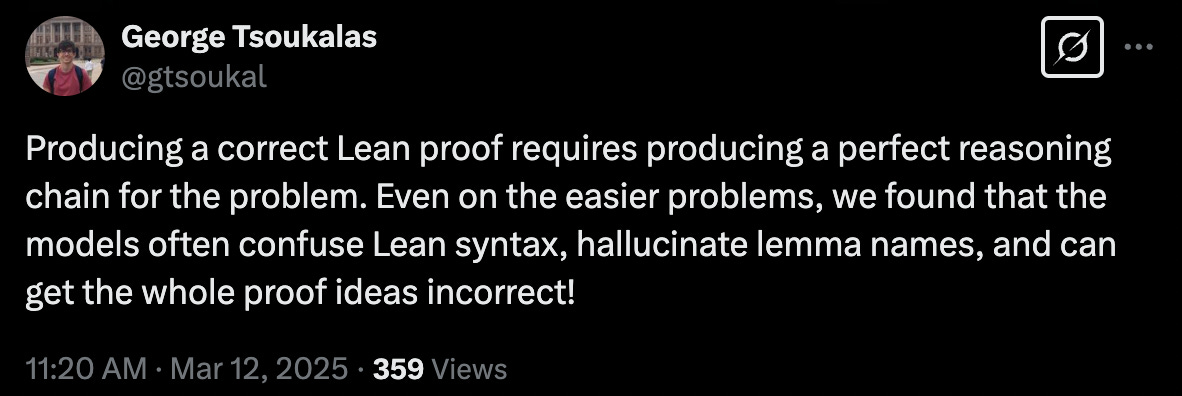
The failure of these otherwise-leading models isn’t so surprising. We already had the sense they didn’t do well on the Putnam in non-formal contexts, and formalization only adds a layer. Indeed, one of the creators of the benchmark had this to say in the way of error analysis:
Strong AI performance on formalized math would certainly be sufficient to show mathematical ability, but it’s not necessary: the vast majority of human math is done without formalization. Formalization is a pretty nascent field and I think the prevailing opinion is that it’s a promising direction but it will take time to mature. For now, humans rely on natural language, albeit with lots of jargon, to express mathematical arguments. We’d be very interested if AI systems could do the same.