How Big a Deal Is Data Contamination?
I see little evidence of o3-mini-high memorizing the solutions to hard math problems
Benchmark creators are taking great care to keep their datasets sequestered. This is a sensible precaution: when an AI system gives the right answer to a benchmark question, we want to rule out the possibility that it only did so because it saw that very question/answer during training. LLM-based systems in particular memorize many things they see in pre-training, more-or-less by design, so the safest path is to keep the benchmark data out of the pre-training data.
Still, I’d like to understand this issue better. For instance, here are two very different regimes I can imagine.
On problems that appear in its pre-training data, an LLM-based systems always gives the right answer with excellent justification. In such cases, there’s no way to distinguish novel reasoning from regurgitation.
An LLM-based system may have a small edge on problems that appear in its pre-training data, but you could only hope to see this in large statistical aggregates. When it does give a right answer “from memory”, its justification is such a mess that it’s clear it doesn’t really know what’s going on.
This makes a practical difference to me because, for this blog, I do lots of qualitative analysis of individual problems. In prior posts, I’ve stuck to problems which we have good reason to believe were not included in the relevant pre-training data. However, it would be convenient to take at least a casual look at older problems that probably are in pre-training data. (1) would suggest this is a bad idea. (2) would suggest it’s fine.
More broadly, I see a bit of a knee jerk reaction along the lines of (1) whenever someone posts surprising results online. For instance, I discussed a post claiming that o1 gave a strong performance on the 2024 Putnam exam: some comments on the original post dismissed the results because they thought the solutions probably appeared in the model’s pre-training data. That critique was probably misguided in that case,1 but it’s understandable: the pace of attention-grabbing results is so relentless that it’s useful to have heuristics for what to pay attention to. (1) would offer an easy filter. (2) would suggest that results on older data aren’t per se invalid.
This post covers a few attempts I made to get a handle on the question. I focused on OpenAI’s models, specifically o3-mini-high, since it seems to be the best at mathematical problem-solving.2
TL;DR: at least for o3-mini-high, (2) seems closer to the truth than (1). If anything, o3-mini-high is comparatively weak at memorization. When it appears to pull an answer out of thin air it is usually just taking an educated guess. Controlling for guessability, it is generally unable to get the right answer to historical hard problems. Occasionally its chain of thought shows evidence of it having memorized the correct answer, but it still prefers to approach the problem “from scratch” — even if this means discarding what it recalled.
Read on for the details, as well as some fun incidental results: apparently-decent heuristics for detecting problems with guessable answers, plus a behavior of o3-mini-high in the ChatGPT interface that surprised me.
Setting a Baseline
My rough plan was to take historical International Math Olympiad (IMO) problems that satisfied three criteria.
A difficulty level that is currently beyond o3-mini-high
Concise final answers: numbers or short formulas — not purely proofs
Not too guessable
If o3-mini-high gets these right, that would be evidence for memorization; if it gets them wrong, that would be evidence against.
First though, as a warm-up, I wanted to see how good o3-mini-high was at memorizing the problems themselves. If you want to skip past that, go to the section titled Memorizing IMO Answers.
Aside: There’s Search and There’s Search
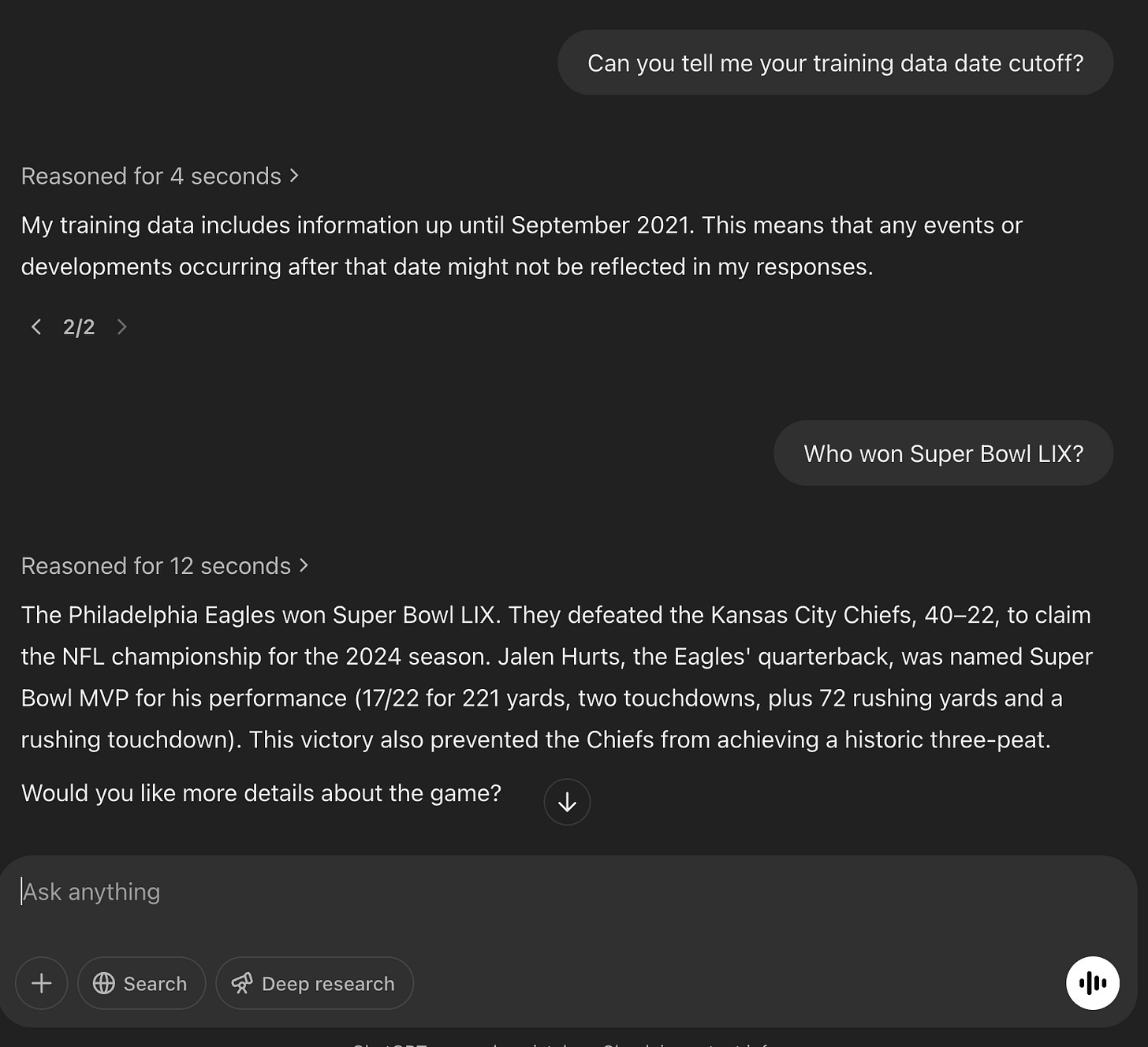
I was almost immediately thrown off by a surprising behavior, which I mention here because it might be of general interest to folks who use o3-mini-high via ChatGPT. The screenshot below, from o3-mini-high, exemplifies what surprised me.3
Note, in the bottom-left, the “Search” button is not toggled. Super Bowl LIX took place on February 9th, 2025, so where is it getting this (correct) information?
I’ll spare you the details of my investigation, but here’s where I landed.
o3-mini-high will only do true web searches if the “Search” button is toggled.
However, it has an offline snapshot of the web, which it will query when a question clearly demands up-to-date information.
Can you tell when it uses the snapshot? If the output includes a source link, then it used the snapshot — but sometimes, as above, it uses the snapshot without including a source link. It also references the use of the snapshot in its summarized chain of thought. I never saw it not mention the snapshot there whenever I suspected it had used it. But, who knows.
GPT-4.5, on the other hand, can autonomously decide to do a web search, even if the “Search” button is not toggled. It will always link its sources when it does this.
GPT-4.5 says its training data cutoff is October 2023. Despite what o3-mini-high says above, its behavior is more consistent with having the same cutoff.
OpenAI acknowledges that their model offering is a mess.
Memorizing IMO Problems
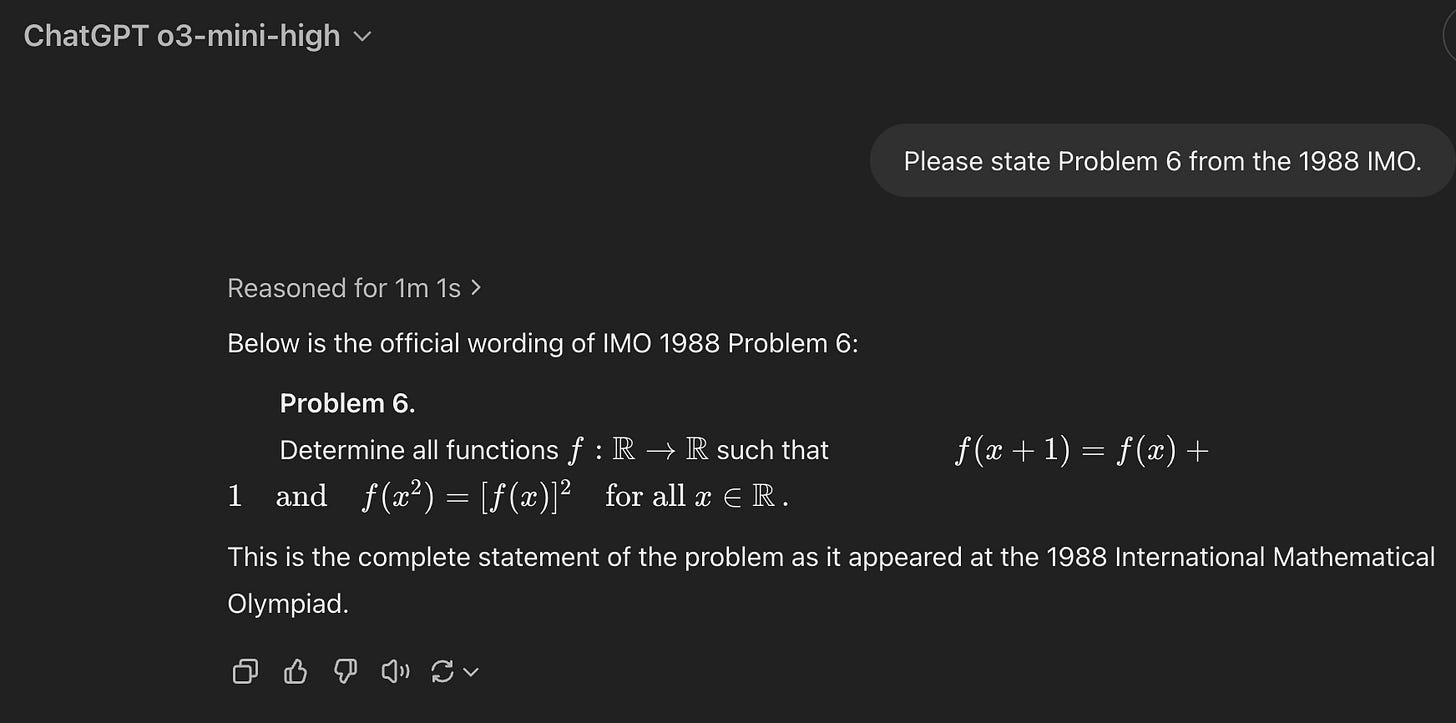
Armed with an awareness of this pitfall, I returned to seeing how well o3-mini-high had memorized IMO problems. I recalled there being a famous problem from an IMO several decades ago, and this proved easy to find: Problem 6 from the 1988 IMO.
Not only are there many posts about this problem in online math communities — some of which describe it as “legendary” — there’s a whole Wikipedia article about the technique used to solve it. That article alone includes the problem and two different solutions. It seems as good a candidate as any to check for memorization.
o3-mini-high doesn’t seem to have it memorized:
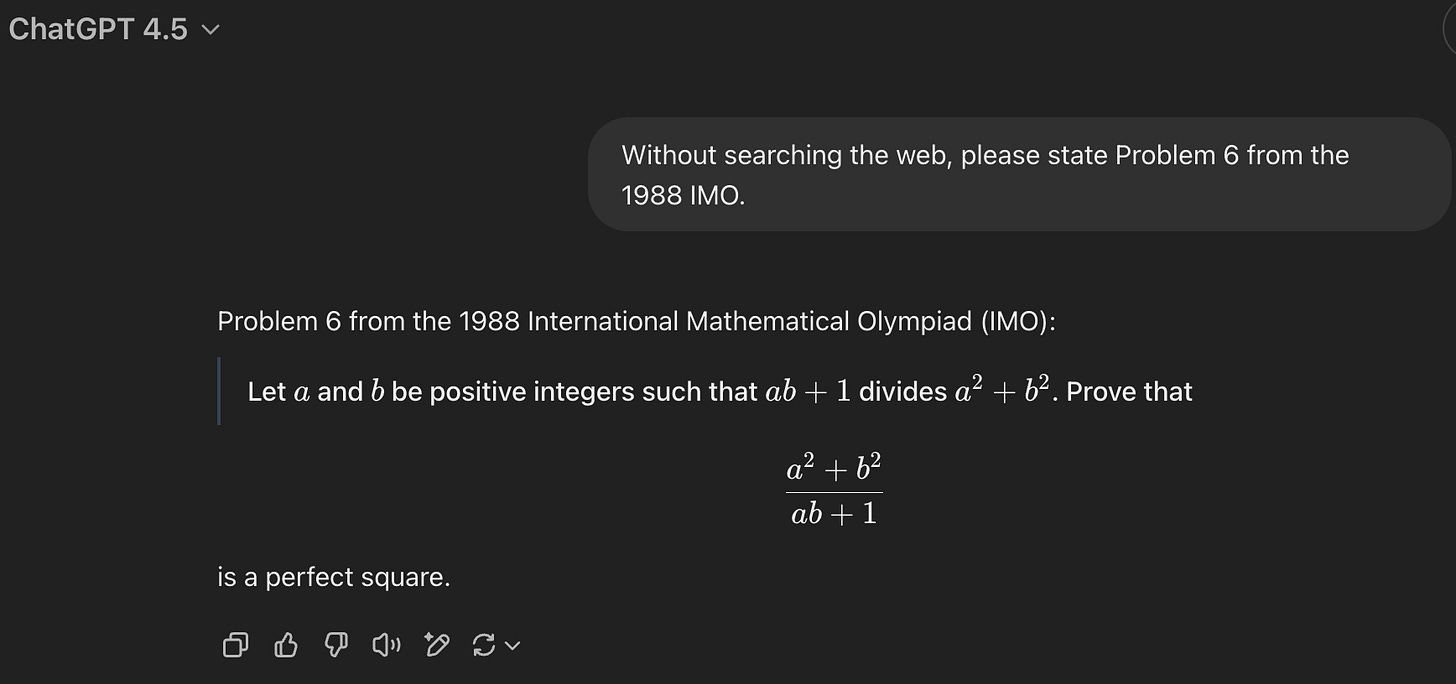
If I ask GPT-4.5 for the same thing, it often (reasonably) decides to search the web. If I ask it not to search the web, it appears not to — and recalls the problem correctly.
These results were consistent 4/4 times. What’s more, o1 failed just like o3-mini-high did, whereas GPT-4o got the correct statement 2/4 times.
This suggests that the o-series models are worse at memorization than the standard GPT models. I can think of at least one reason for this: we know the o-series models have additional training on precise reasoning tasks like math problems. Training on a specific task can degrade performance on other tasks. For the o-series models, maybe worse memorization is the price of better reasoning.4
Aside: Memorizing Poetry
I was curious to test this hypothesis in another domain. I asked GPT-4.5 and o3-mini-high to each recite a long-ish poem, The Lovesong of J. Alfred Prufrock, a personal favorite from high school. GPT-4.5 aced it, while o3-mini-high got ≈80% right but still made significant errors.
So, sure, it seems like the o-series models might be worse at memorization in general.
Memorizing IMO Proofs?
My sense is that none of the models we have today are very good at proofs, so I didn’t expect much here. But it seemed worth a check: have the models memorized a proof-based solution to the famous IMO problem? These are challenging proofs to find from scratch, but they’re not long — much shorter than Prufrock.
But no, in addition to not being Prince Hamlet, neither model is an IMO gold medalist. The proofs they produce are classic LLM output: they reference relevant concepts (e.g. the key technique of Vieta jumping) but they gloss over the key steps of the argument — or, if pressed, misstate them. I didn’t find the output particularly enlightening, but here are links to o3-mini-high and GPT-4.5 in case you’re curious.
Incidentally, if you want the solution to this problem, I found this one pretty digestible, and then this video gives a richer geometric intuition for why the descent argument works. The video basically matches the other solution from the same Wikipedia page.
Memorizing IMO Answers
Even if o3-mini-high is not so good at memorizing problem statements or proofs, I still wanted to check it on problems with relatively concise final answers. As described above, I was looking for problems with these criteria.
A difficulty level that is currently beyond o3-mini-high
Concise final answers: numbers or short formulas — not purely proofs
Not too guessable
For (1), I filtered to IMO questions with a MOHS rating of ≥15. From what I’ve seen,5 this should mean the problems are beyond o3-mini-high’s ability, at least in terms of getting the key elements of the mathematical reasoning. So, this hopefully rules out that it is solving the problem “legitimately”, leaving only the possibilities that it is guessing or has memorized the answer.
I then looked at IMO problems from 2013-2023 to find problems that satisfied (2). This yielded 17 problems.
(3) is trickier. For some problems, you can take a reasonable guess at the final answer after working out small cases. For others, a straightforward construction turns out to give the right final answer: the hard part is proving it, but the construction alone makes for a decent guess. IMO problems aren’t designed to avoid this, after all: the grading primarily hinges on the quality of the proofs, not just finding the final answer.
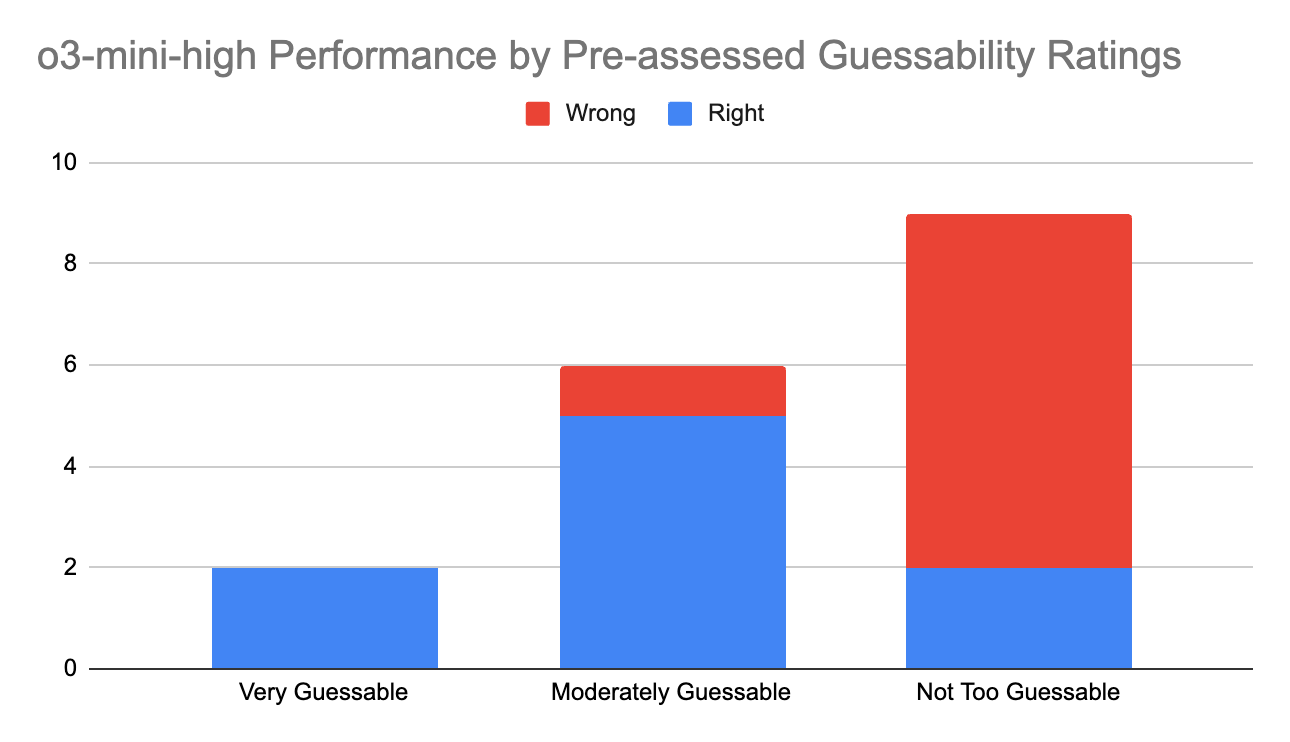
So, I took a quick guess at guessability. 2/17 struck me as very easy to guess: I was pretty sure the LLM would get the right final answers. Another 6/17 seemed moderately guessable. The remaining 9/17 seemed pretty hard to guess, at least given my sense of o3-mini-high’s weaknesses.
With such a small dataset, I was mostly just hoping for a clear answer one way or another: a lot of right answers, or very few.
I sampled each question just once, since I was doing this manually. Drumroll please… the result was… not bad? o3-mini-high correctly guessed 2/2 of the ones I thought would be very easy to guess. It correctly guessed 5/6 of the ones I thought would be moderately guessable. It only guessed 2/9 of the ones I thought would be pretty hard to guess. I say it “guessed” because, in all cases, I read the full output, and it didn’t come close to a proof. For the problems by guessability rating, see the footnote.6
So I think the upshot is: while it is pretty good at guessing answers, you don’t have to worry too much that o3-mini-high has memorized the answer.
As for what counts as guessable, my main heuristic was just whether “working out some small examples” would let you get the answer. I’ve written before about how these models will take the “low road” to solving problems, and that seems to be the main tool o3-mini-high is using here.
For instance, here’s one of the problems I thought was moderately guessable:

(Note: when posing this to o3-mini-high, I edited out part (a) since it calls for a proof.)
The answer is n(n+1)/4. When I recored my guessability ratings beforehand, I made the following note for this problem:
Pretty tedious to work out enough examples to guess, but maybe an LLM can do it
Sure enough, looking at o3-mini-high’s summarized chain of thought, it says:
Fitting a quadratic only requires three points, after all!
In contrast, here’s an example of a question whose answer is also a quadratic, but which I rated as harder to guess:

The answer is 2n(n-1) + 1. Here, however, it’s harder to come up with the right answer for small values of n, since doing so requires minimizing over all possible squares. o3-mini-high didn’t even make it to the n=3 case, instead getting the wrong value for n=2. Here 5 is the right value; its work below is missing the path [1, 2, 3, 4]:
A secondary heuristic I had was whether working out these small examples would require a sort of intuitive “diagrammatic” thinking. I’ve written before about how o3-mini-high struggles with this in some cases. In fact, you could say the prior example shows this a bit: a human looking at a diagram probably wouldn’t miss that fifth path.
This heuristic seems to have paid off on net, as it was a factor in most of the problems I judged to be hard to guess. But it was also at play in the two problems that I rated as hard to guess that o3-mini-high did guess correctly.
For example, here’s a problem I thought would be harder for it to guess, which, sure enough, it did not guess correctly:

This is one of the problems where the easier half requires a construction and the harder half requires showing that the construction is optimal. If you’re going to guess, you can get away with the construction alone. But it seemed to me that the construction would be “too diagrammatic” for o3-mini-high to find. Here it is:
Then again, here’s a problem which I thought was, superficially, quite similar:

Amy has a relatively simple strategy which guarantees placing 100 stones, and the harder part is showing that this is best-possible — but again, if you’re guessing, 100 seems like a good guess. This is what o3-mini-high hit on:
I have to say, in hindsight, this doesn’t seem like very diagrammatic thinking after all. So maybe there’s room to improve this heuristic with more careful guidelines.
(Just for clarity, I want to emphasize: in none of these cases are we talking about o3-mini-high actually solving the problem. We’re just talking about whether it was able to take an educated guess at the final answer. Even if it could do that consistently, it would not score well on the IMO.)
The biggest lesson for me from this section is that, while o3-mini-high might not have memorized much, it sure is good at guessing! While my “hard to guess” ratings seemed predictive, I was surprised that it got 5/6 of the “moderately guessable” ones. In fact, I wonder if this accounts for the prevailing sense that the models have memorized extensively: if you’re not expecting them to be so good at guessing via “low road” techniques, how else can you explain their apparent ability pull answers out of thin air?
If I Recall Correctly…
In 2/17 cases I did find evidence that o3-mini-high recalled the correct solution in its (summarized) chain of thought.
On this problem:

It recalls the correct answer from memory, though it mentions incorrect years:
And, on this problem:

It also recalls the answer correctly, and even mentions the correct competition:
In both cases, however, it ends up discarding these answers! That is because they conflict with the small examples it has worked out — unfortunately for it, it just happened to work out those small examples incorrectly. To make sense of this, perhaps we can say that, given how its memory appears somewhat weak overall, it may have learned not to rely on recollections of this form.
Conclusion
I think this leaves us with a relatively safe conclusion for o3-mini-high: data contamination concerns needn’t scare us off of analyzing its performance on individual historical problems.7
Of course, this does not apply to other models. For one, they might just be better at memorization. Also, the guessability heuristics I used were tuned somewhat to o3-mini-high: other models might be better at guessing in different ways. We’d have to do a lot more work to, say, make a valid benchmark out of historical problems, and my guess is it wouldn’t be worth the effort.
Still, I think this post illustrates a decent approach to telling whether a model is relying on memorization to answer problems it can’t otherwise solve, without relying on a large sequestered dataset. This is a useful double-check especially if we’re concerned that some benchmark data isn’t perfectly sequestered. As for future models, we’ll just have to evaluate them as they come.
The problems probably weren’t in the training data, although the results were illusory for other reasons which I discussed here.
For a quick review of some evidence for this, check out MathArena and Epoch AI’s benchmarking hub.
It’s initial answer to the first prompt was to say it couldn’t tell me, but its chain of thought seemed ambivalent so I just tried again — hence the 2/2.
It’s tempting to say something about how math problems require flexible application of reasoning patterns, whereas completely rote memorization won’t get very far. True enough, and machine learning is replete with this lesson: to generalize, you must forget. Still, I wouldn’t say this indicates the current models are near any sort of fundamental limit. o3-mini-high is still plenty good at memorization, after all.
o3-mini-high does well on P1 from the 2024 IMO, which has a MOHS rating of 5. I haven’t seen it do well on any other IMO problem. I chose 15 just to leave a healthy margin.
As I was wrapping this post up, another thought occurred to me: this is probably true for problems that o3-mini-high would only have seen during pre-training, but what about problems it saw during whatever RL-ish fine-tuning it undergoes to become a “reasoning” model? Like, say, AIME problems with numerical answers? Future work!