Proof Left as an Exercise for the Reader
Gemini 2.5 Pro shows some promise at judging its own proofs
I’ve written before:
Wouldn’t it be interesting to give an LLM a large set of unsolved math problems — most of which require proof to resolve — just to see what it came up with? Well, it sounds interesting, but it would still be a slog to go over all those attempted proofs. Most of them would be junk; they might all be junk.
Gemini 2.5 Pro seems to have a better handle on proofs. The spot check I did in the previous post to see whether it could tell that its own proof was inadequate gave mixed results, but I wanted to see if I could get it to do better.
Another reason to investigate this is it might give us a deeper sense of the model’s latent proof-writing capabilities. If we loosely model proof-writing as generating candidate proofs (or proof steps) and then judging whether they are valid, this exercise directly tests the judging capability. In many contexts, generating is harder than judging: this is the crux of P vs. NP, after all. Thus, a very good judging function doesn’t get you a proof: you just spend all day debunking junk. But there’s a bit of a spectrum too: a marginally better judging function should let you get away with a marginally worse generating function. Certainly if the judge is very bad, the overall system won’t be good either. It’s worth a look, anyway.
This post covers a small-scale experiment trying to get Gemini1 to judge its own proofs.
TL;DR: It’s not too bad! There’s some signal in asking it to self-report when it has failed to solve a problem, and there’s additional signal in getting it to review its own attempted solutions. It can still struggle with subtle logical flaws, and probably more filtering is needed when it cites results from the literature. But overall it seems to have enough of a basic capability that I could believe there is utility to using it in this way.
Round 1
I started with 12 problems: the 2024 IMO and the 2025 USAMO. These don’t always ask explicitly for proofs. They might just say, for instance, “Find the smallest integer such that…” But contestants all understand that, on these competitions, proofs are required. To remove ambiguity, I added the phrase “with proof” to such cases, for instance editing “Find” to “Find, with proof,”.
I then added the following after the problem statement, so there would be an easy-to-find indication that it thought it had failed:
If you cannot prove the statement rigorously please conclude by saying, "A complete proof was not found."
I played around with the wording but didn’t see much variation on a few test cases.
Here are the results, based on my own judgement of its output.
3 True Positives (TP): didn’t report failure, and was right not to
6 False Positives (FP): didn’t report failure, but should have
3 True Negatives (TN): reported failure, and was right to
0 False Negatives (FN): modesty is not a problem
Half of the samples being false positives is not so good. I noticed, though, that Gemini sometimes gave a pretty strong cue that it had failed, despite not reporting it the way I had asked. For example, on 2025 USAMO P3, when trying to prove that Bob wins:
That sure sounds like it’s missing a full proof. Odd that it can’t pick up on that when self-reporting, but maybe a second round can do better.
Round 2
In the spot-check I had done previously, I asked it to rate its own proof on a standard competition grading scale. But maybe that was needlessly complex. I tried a simpler binary prompt here, in a fresh session for each problem where it hadn’t reported failure (i.e., TP + FP):
Here is a math problem: [problem]
Here is a proposed solution: [AI solution]
Does the solution constitute a largely-complete proof or are there significant gaps? Please conclude your answer either with, “The proof is largely complete.” or “The proof has significant gaps.”
That actually helped quite a bit! The true positives were all judged to be “largely complete”. 4/6 of the false positives were judged to have “significant gaps”.
Of the 2/6 persistent false positives, one seems nearly fine. Here’s what it says—you don’t need to know the problem statement to follow its discussion, just that “all even integers” is indeed the correct final answer.
This is indeed a competition question, and, anyway, as far as I can tell, the citations are all made up. So this seems like something that further prompting or scaffolding could resolve in whatever way was desired.
The other persistent false positive is, my favorite, Turbo the snail from the 2024 IMO. Here it does identify a gap in the proof, but judges the gap to not be critical.
I wonder if part of what is going on here is it thinks the solution gets the right final answer and therefore cuts the proof some slack. I’m sure humans would be liable to this bias, anyway.
To its credit, it doesn’t always make that mistake: in the second-round judgement it sometimes does state that the answer is right but the proof is wrong. For instance, here it is evaluating the solution to 2024 IMO P6:
The right final answer is actually c=2, not c=1. So it’s wrong about that in both the first and second round. However, in the second round, it is right about the logical flaw.2 So, it’s good that it’s judging the proof correctly and independently of the answer. Still, given the result on the Turbo the snail problem, I wonder if these sorts of judgements are less robust.
The Competition
Just to see, I tested o3-mini-high in the same setup, in case these exact prompts—which I hadn’t tried before—also helped it. Its initial results had the same number of false positives:
1 True Positive (TP): didn’t report failure, and was right not to
6 False Positives (FP): didn’t report failure, but should have
5 True Negatives (TN): reported failure line, and was right to
0 False Negatives (FN)
But the second-round filter only corrected one of those false positives: 5/6 times it stated that the solution was largely complete. This is consistent with what I’d described before about how it seems to like its own proofs. So I do think Gemini might have something new here.
Out-of-Sample Test
I mucked around a bit to get to the methodology described above, so it’s good hygiene to try it on some unseen data. For this blind test, I used the 2024 Putnam, a undergraduate competition whose difficulty range is roughly comparable to the USAMO and IMO. The Putnam consists of two sets of six questions, denoted A1-6 and B1-6. Problems increase in difficulty within each set.
The two rounds of filtering didn’t catch as much.
2 solutions failed the first filter (“A complete proof was not found.”): B2, B5
2 more failed the second filter (“The proof has significant gaps.”): A3, A5
8 passed both filters: A1, A2, A4, A6, B1, B3, B4, B6
I’m presenting these without the T/F P/N labels at first because I’ve spent less time with these problems and want to emphasize that my grading could be wrong. I’m using this solution guide, but Gemini’s solutions don’t always match perfectly—it often takes a “low road” approach, as I’ve discussed—and the difference between a correct proof and a totally wrong proof due to a single mistake can be very subtle.
But anyway, how many of those 8 passes do I think are correct? A lot, actually!
Starting with the A-problems, Gemini’s solutions to A1, A2, A4, and A6 all look good. Beyond my grading, we can also consider some general expectations. A1 and A2 should be comparable to the easiest problem on the USAMO/IMO, which we know are within Gemini’s reach. A4 might seem suspicious, but the stats for human contestants show that A4 was uncharacteristically easy this year. On A6, it seems like Gemini is getting away with some background knowledge. Here’s the problem:
And here is the heavy-duty tool Gemini produces from memory, to crack it:
This appears to be fair game: the solution guide I’m using mentions that its solution draws explicitly from prior art:
Indeed, if I ask Gemini to cite a source for its formula for the determinant of a Hankel matrix, it gives a list with this at the top:
That is amazing in its own right. Even so, we must say that the difficulty of this problem stems in significant part from the background knowledge required, and that this is much less of an obstacle for Gemini than for a human contestant.
Moving on to the B-problems. B1 looks good, and a correct solution isn’t surprising. On B3, I’m not sure: Gemini’s proof looks ok to me, but it’s a bit of a slog to check, and I could have easily missed a mistake. It also doesn’t match either solution in the solution guide, though it’s possible it’s just taking more of a “low road” approach than the guide author was inclined to include. B4 is again atypically easy, requiring a relatively straightforward computation which Gemini appears to do just fine.
B6 is funny. Here Gemini approximates a sum with an integral and gets the right final answer. But it seems to know that it doesn’t quite have a rigorous proof. Looking into its chain of thought, it wraps up with this amusing comment.
The solution guide does indeed give a more rigorous proof, constructing explicit upper and lower bounds on the sum in question. That said, as long as I’m not missing any logical errors (big if), I think Gemini’s solution probably does count as a good heuristic argument. In any case, I’m only giving the summarized solution to be judged in the second round, not the whole chain of thought.3 Presumably Gemini-as-judge would pick up on comments like the above if they were included.
Putnam? I ‘ardly know ‘im!
It’s a tangent, but, if I didn’t mess up the grading too badly, Gemini did better on the Putnam than I would have expected! I mostly attribute that to my being unfamiliar with the test. Some of its harder problems seem more amenable to low-road execution-oriented approaches and background knowledge application than I had thought. I’ll have to revise one of my predictions here: Gemini seems to have a good shot at cracking 50% on the Putnam. I’d put my 95% CI at something more like 1/3-2/3. No changes to the other predictions.
Out-of-Sample Conclusion
Anyway, where does this tally leave us in terms of proof rating?
7 True Positives (TP): didn’t report failure, and was right not to
1 False Positives (FP): didn’t report failure, but should have
4 True Negatives (TN): reported failure, and was right to
0 False Negatives (FN)
I could easily believe I mis-graded a few problems, so maybe we conservatively imagine it’s more like 5 TP / 3 FP.
Regardless, I think this bodes pretty well for Gemini using this methodology, at least as applied to competition-style problems.
The Unsolved
At this point, we’ve got to try it out on some unsolved problems. I randomly sampled 6 problems from this site, which is a catalog of (as of this writing) 944 problems posed by hyper-prolific mathematician Paul Erdős and categorized by whether they have been solved or remain open. These problems are all probably too well-trodden for Gemini to have any chance at even a single one, but it’s a fine way to test our methodology.
Here are the results.
4 failed the first filter (“A complete proof was not found.”) 810, 82, 580, 313
1 failed the second filter (“The proof has significant gaps.”): 413
1 passed both filters
The first filter is doing the bulk of the work, reflecting how Gemini can tell that the problems are hard. For example, here are its comments wrapping up 580:
Also, as I mentioned before, its command of the literature means that it sometimes knows the problem is unsolved. Here it is on 313:
For humans, anyway, I think this can lead to an intimidation penalty. If there is an easy solution that has escaped other mathematicians you’re more likely to find that if you don’t know that it’s an allegedly hard problem. Who knows, but I wonder if LLM-based systems are subject to the same dynamic.
Ok, but what about the problem that passed both filters? Here’s the statement:
This problem seems very well-covered in the literature. A positive resolution was conjectured first by Hindman, who showed that if A is infinite then the statement is false. It’s still an active area of research. In 2023, it was shown by Alweiss that the conjecture is true if N (positive integers) is replaced by Q (rational numbers).
If I’m reading this right, Gemini’s solution hinges on citing a result from the literature that directly implies the conjecture.
This cited result is probably just fictitious. At least, I can confirm that it is not in fact Theorem 17.16 in the given textbook.
The second-round filter has this to say:
So, it doesn’t check the cited result, but it does see that the proof relies on it entirely.
That’s somewhat promising, I think, because it might be possible to check in a further filtering step whether any critical cited results are real. I tried excerpting this citation in a fresh session and asking Gemini if the result was correct. Without Search enabled, it said it was correct—maybe that makes sense, since it confabulated it in the first place. But with Search enabled it correctly said that the result was incorrect, though I’m not sure if its discussion is correct (that’s not what the Milliken-Taylor Theorem looks like on Wikipedia, anyway).
Still, this might mean it’s possible to automatically check the quality of citations, perhaps in a third filter step. We’d probably want to implement something like that before trying on a larger set of unsolved problems.
Conclusion
Gemini 2.5 Pro’s grasp on what makes for a valid proof is strong enough that it is able to self-assess its own proofs pretty well, and better than I’ve seen from other models.
I wouldn’t hold my breath for it to solve even a single Erdős problems, but the methodology described above might help make it more useful on routine problems encountered in the day-to-day of math research. At any rate, if a mathematician wants to toss a small subproblem to Gemini, I would suggest trying something like the prompts above to get it to self-filter.
And if anyone has a repository of less-well-known unsolved problems, I wouldn’t say no to a chance to try out the above methodology at scale!
As for projecting future capabilities, I would say this ability is a useful ingredient to solving harder math problems, but I wouldn’t jump the gun. You have to know whether your working solution is right or wrong in order to find a correct one, but the harder part by far is coming up with the right ideas in the first place.
For brevity, I’ll sometimes abbreviate “Gemini 2.5 Pro” to “Gemini” in this post. No other model was used unless explicitly noted.
I don’t see a good way to link to a Google AI Studio chat, so, details happily available upon request!
GDM doesn’t seem to be obscuring the chain of thought at all—great for research purposes!






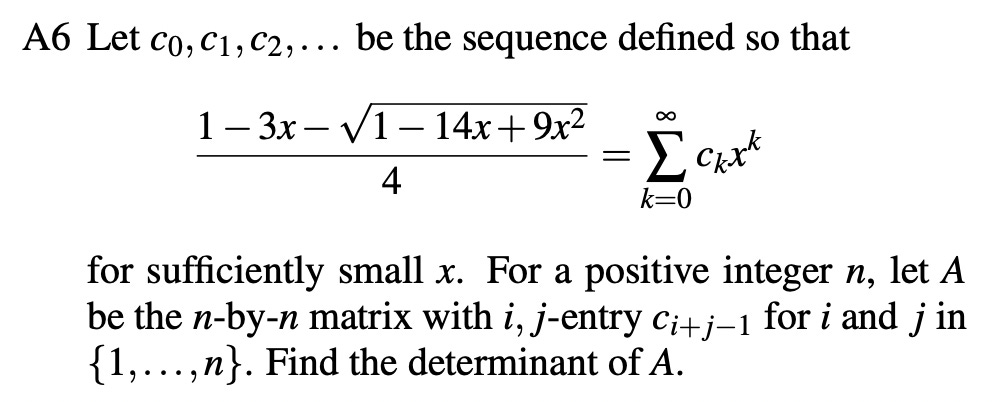











Great article. But it's crazy to me it can do anything approaching what you've written about here and still fail at judging simple river crossing puzzles (like the ones Colin Fraser posts). I asked it this:
"A baker needs to get across a river with his prize pig, his hound, and five loaves of bread. The boat has enough room for the steerer, a single animal and a single loaf (they're big loaves). The pig will eat any loaf that it's left alone with. The hound will attack the pig if left alone with it. How can he get across the river in the fewest trips with all his possessions fully intact?"
It mapped out every step (the proof, if you will) and said the minimum number of trips was 13, though 11 is clearly possible. It insisted even when prompted to double check.
I'm sure it must get the answer right sometimes, however, the USAMO this is not. My theories on this kind of failure are no different from anyone else's, but I do want to emphasise that it's wacky as hell.