AlphaProof and the IMO

Harder problems, formal proofs, and still perhaps a creativity deficit

This blog has focused on a particular kind of AI system: broad-based LLMs that have been post-trained on reasoning tasks. I’ll refer to such systems as Reasoning LLMs (RLLMs). What’s so compelling about RLLMs is their generality. Even just in math they show promise at a wide range of tasks: problem solving of course, but also literature review, code generation, and more.

Still, there are a few math tasks where other computer systems are clearly better. The most obvious is intensive numerical calculation: even a calculator beats an RLLM at arithmetic. The path there is clear, though: it’s ok if RLLMs aren’t good at doing calculations themselves so long as they can use special-purpose systems as tools.

There is one area, however, where I think the path is less clear: what will be the future relationship between RLLMs and formal proofs?

By formal proof, I mean a proof written in a special-purpose programming language that can be verified by a special-purpose computer program. By way of background: mathematicians first invented these systems to check their work. If you have a long and complicated proof, how do you know it’s right? You review it many times, other mathematicians do as well… and, for a while, that was it! You might very reasonably worry that everyone had missed something. But, if you encode the steps of the proof in a formal, logical language, then a verification program can say whether the proof has any gaps. This doesn’t address every source of error (e.g., bugs in the verification program itself) but as a practical matter it’s a big improvement.

Formal proofs are also very appealing as a target for the output of AI math systems. As we’ve discussed, a big problem with RLLM proofs is that they are informal, and thus might contain subtle flaws. While RLLMs show some promise at self-critiquing, it would be much easier if we could just get formal proofs.

And indeed, there has been some progress on special-purpose AI systems that generate formal proofs. I’ll refer to such systems as Formal Proof Models (FPMs). Probably the most impressive FPM is AlphaProof by Google DeepMind (GDM), which generated formal solutions to 4/6 of the problems on the 2024 International Mathematical Olympiad (IMO)—including one of the two hardest problems. By contrast, every RLLM that I’ve tested can, at best, generate an informal solution to the easiest problem.

So, the best FPMs have some math capabilities that the best RLLMs do not, and this remains true even if we only judge the RLLMs on their informal outputs. Should we expect RLLMs to get much better at generating formal proofs, or will they end up outsourcing this task to specialized FPMs?

It seems plausible that RLLMs could catch up. After all, we use RLLMs to generate code, and formal proofs are just a kind of code. The formal verifier can provide a reward signal during an RLLM’s post-training, and this can be scaled up easily. RLLMs can also use their general math knowledge, derived from natural-language math, to help guide formal proof construction—a signal which FPMs may lack.

But it’s also not hard to imagine FPMs staying ahead. While RLLMs could be trained using the formal verifier, it doesn’t seem like they could make too much use of it at runtime. They might have a “loose outer loop”, where they write a proof, check it in the verifier, and then try to rewrite as needed. But it seems likely that different architectures would let an FPM use the verifier at runtime in more of a “tight inner loop”, and that difference could be decisive.

I’d usually bet on the specialized system beating the general purpose system, at least given the same budget. But when it comes to proofs, I do think the RLLM’s general knowledge could be very helpful. And, if RLLMs are scaling up anyway, the results “on the same budget” might not be relevant.¹ Really I shouldn’t even imply that “RLLM vs. FPM” is a binary. For instance, a special-purpose proof generation system could involve an RLLM in its architecture. Or, maybe there’s a way to incorporate a verifier into some sort of inner loop even in an RLLM. That’s all just to say, I don’t know how these systems will co-evolve.

But, so long as AlphaProof is solving IMO problems that the best RLLMs cannot, I think it’s worth looking at that performance specifically. That’s what I’ll do in the rest of this post.

TL;DR: I didn’t find what I expected. AlphaProof’s solution to the one high-difficulty problem was a complete grind. The one medium-difficulty problem it got was a bit more interesting: it found the necessary “trick” and did the right thing with it. But, given that trick as a hint, o4-mini-high can solve it too, at least informally. The medium and hard problems that AlphaProof didn’t solve are, to my eyes, the ones that require deeper understanding and more creativity. I’m left wondering whether frontier math systems, be they RLLMs or FPMs, are essentially similar: their training lets them grind out essentially straightforward solutions—but anything that humans would consider creative remains out of reach.

It’s hard to predict how these systems will evolve because it’s unclear when they will get past where they are now. That said, thanks to the formal verifier, AlphaProof might be easier to scale up. We know that game-playing systems trained with reinforcement learning (e.g., AlphaGo) have been judged by humans to be brilliantly creative. Maybe AlphaProof will surprise us at the 2025 IMO.

What Is AlphaProof?

There aren’t that many primary sources on AlphaProof. For this section I’m drawing primarily from the GDM blog post announcing the project and from this recent presentation by Thomas Hubert, a researcher who worked on the project.

AlphaProof generates proofs in a formal language called Lean.

The core of AlphaProof is AlphaZero, the same reinforcement learning algorithm that GDM used to make superhuman game-playing systems like AlphaGo. My basic understanding of AlphaZero is that it has a “move evaluator” neural network, which predicts how successful a single next move will be. This is used to guide a Monte Carlo tree search (MCTS), which lets the system look further ahead than a single move. The move evaluator is the part that gets trained. This is done by having the whole system play itself and updating the neural network’s weights based on each game’s outcome.

To map this to formal proofs, think of the “moves” as steps in the proof: new lines of Lean code. You “win” if the verifier accepts the finished proof.

Unlike with self play, though, training can’t happen totally from scratch: the system needs problems to solve. This is one place where GDM used a language model: they fine-tuned a Gemini model on Lean data, and used that to translate natural language problem statements into Lean. It isn’t perfect: the formal output doesn’t always match the meaning of the original natural language. But that doesn’t matter: they just needed a lot of problems stated in Lean.²

For the “move evaluator” they used a different language model, which they call the prover model. They trained this on the main Lean library, presumably with a standard language modeling objective.³ This gives it a general feel for Lean, including the common “moves” to make. They then further trained it with the AlphaZero reinforcement learning algorithm, using the problems generated in the previous step.

There’s one more step, which Hubert suggests is crucial. From the blog post:

The training loop was also applied during the contest, reinforcing proofs of self-generated variations of the contest problems until a full solution could be found.

In other words, AlphaProof generated variations of the problem and tried to prove those too, letting any successes update its weights—but just for that problem. It thus adapts itself differently to each problem. This is relatable to humans: when you’re stuck on a problem, one approach is to try solving a slightly different problem. That can shed light on the original problem, or, at least, give you some new ideas to try.

That’s the big picture, and I think it gives a decent sense for how AlphaProof works, but there are two more details about how it actually gets applied to IMO problems.

First, problems aren’t always statements: sometimes they say things like “find the smallest integer such that…”. In such cases, you have to come up with an answer first (e.g., a specific integer) and then prove the resulting statement. For this, AlphaProof uses Gemini to generate many candidate answers, and then tries to prove/disprove each one. This is enviable from a human perspective: if only you could control your mind enough to focus entirely on proving a particular candidate answer, and then, if unsuccessful after some time, wholly focus on a different candidate answer.

Second, the actual IMO problems come in natural language.⁴ Since the formalization into Lean is error-prone, GDM formalized the problem statements by hand. This is certainly a weak spot of the project, though I think it doesn’t really detract from the accomplishment. Autoformalization can be improved separately, and mathematicians probably wouldn’t mind if the cost of getting superhuman formal proof generation was just putting problem statements into Lean by hand.

What About AlphaGeometry?

GDM has a completely separate system for solving Euclidean geometry problems, which are a staple of high school math competitions. The original such system was called AlphaGeometry, and an improved version, AlphaGeometry2, was used on the 2024 IMO. It so happens that there was only one geometry problem on the 2024 IMO, a relatively easy one, and AlphaGeometry solved it quickly.

I won’t be covering AlphaGeometry in this post. This is partly just for brevity’s sake, but also because I don’t think its success is as interesting as AlphaProof’s. My sense is that Euclidean geometry is a fairly constrained domain: everything is just points, lines, angles, and circles, with standard relationships among them. What makes problems tricky is that you have to add just the right elements to the picture. Once you’ve done that, you work through deductions via the standard relationships until either you’re done or you’re stuck—and, in the latter case, you rinse and repeat.

While this can be very challenging for humans, especially when on the clock and especially when many stages of addition and deduction are required, the possibility space just doesn’t seem overwhelming. Maybe exhaustive search isn’t possible, but I’m not so surprised that a mix of heuristic and learned search gets pretty far.

The 2024 IMO

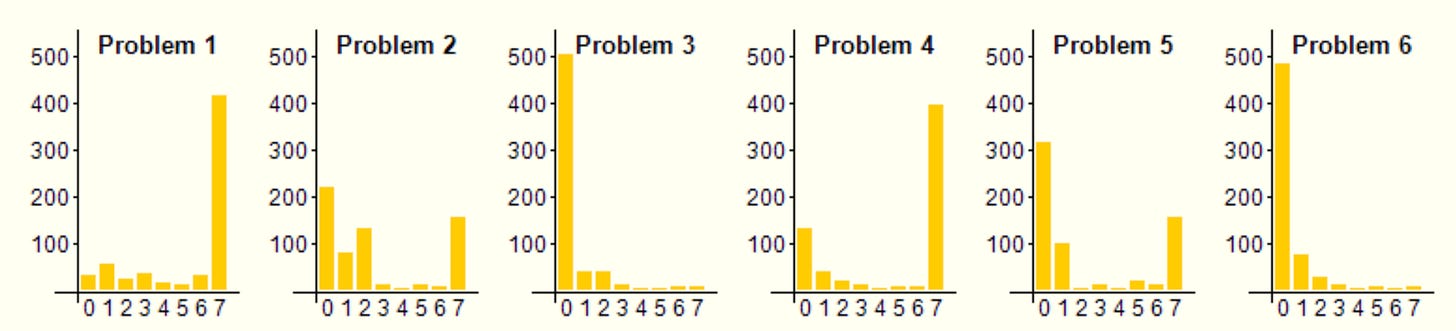
On to the problems! The IMO spans two days, with contestants given 4.5 hours to solve three problems on each day. The problems on each day are ordered roughly by difficulty. Each country sends a team of six contestants, all of whom take the test individually. Solutions take the form of natural language proofs and are graded by human experts. Each solution is scored on a 0-7 scale, with partial credit given sparingly. Here are the score distributions for the 2024 problems.

Source

As you can see, most contestants got P1 and P4, the distributions for P2 and P5 are bimodal with about 1/3 getting full credit, and almost no one got P3 or P6.⁵

P1 is the easiest problem. Not only did AlphaProof get it, but the best RLLMs can get it as well, at least informally. Again for brevity’s sake, and since it doesn’t distinguish AlphaProof as much, I won’t cover it in this post. P4 is the next-easiest. It happens to be the one geometry problem, and AlphaGeometry2 got it.

That leaves medium-difficulty P2 and P5, and hard P3 and P6. Conveniently, AlphaProof got one of each: P2 but not P5, and P6 but not P3. That lets us make a bit of a difficulty-adjusted comparison: what makes a problem hard for AlphaProof, even adjusting for human difficulty? I’ll delve into all of this below. Be careful scrolling if you want to avoid spoilers: I’ll discuss solutions immediately after the problem statements.

Sequence of GCDs (P2)

That is, for which (a,b) is the sequence gcd(aⁿ+b, bⁿ+a) eventually constant.

This is one of the problems that isn’t provable as stated: you have to prove that the answer is some specific set of pairs of positive integers. In fact, the answer is the trivial set: the only pair that works is (a,b) = (1,1). Luckily for AlphaProof, that’s probably pretty easy to guess: (1,1) obviously works, nothing else obviously works, so you might guess that that’s it.

Now, how to prove it? The key is to consider things modulo ab+1. To my eyes, there’s sort of a “dumb” reason to try this: you might want to see if you can use Euler’s theorem on both aⁿ and bⁿ, but for that to work you need something coprime to both a and b, and ab+1 is a natural candidate. There’s also a smarter reason, see footnote.⁶ In the words of the problem’s author,

Once you realize you should be working with this quantity, I think you should be able to solve the problem immediately.

That’s probably inflected with hindsight, but the point is there’s nothing especially tricky if you pursue the “ab+1” path: from there, you need to hit on the right algebraic manipulations, but you are likely to find them with some diligence.

AlphaProof’s solution more or less matches what is, in my opinion, the nicest of the official solutions (Solution 3 on page 12 here). The only oddity is how it orders things: first it proves the conditional that, if ab+1 divides g, then a=b=1; then it proves that ab+1 divides g. I think a human might not jump to proving a consequence of ab+1 dividing g before actually proving that ab+1 divides g, but maybe MCTS gives AlphaProof enough “intuition” that its approach will pan out.

Or, that’s the only conceptual oddity. Its Lean code is also quite ugly by human standards. There’s no reason for it not to be, since its only objective is correctness. If anything, I would guess it can more easily find shorter proofs, and compactness sometimes runs against comprehensibility. You’d certainly hope that an RLLM could clean this up somewhat, though I didn’t get good out-of-the-box results when I tried.

I’m no Lean expert, but I don’t think it’s supposed to look like this.

Anyway, though: well done, AlphaProof. I mentioned that o4-mini-high and Gemini 2.5 Pro can’t solve this problem. Really what I should say is that I haven’t seen them solve it in the ≈dozen samples that I’ve tried. AlphaProof has the clear advantage here: it can sample as many times as it wants, and if the Lean verifier accepts any one of its attempts, it wins.⁷

Still, given the relatively short “key idea”, I tried giving o4-mini-high and Gemini 2.5 Pro this hint:

Consider things mod ab+1, finding a suitable n>N to apply Euler's theorem.

Gemini didn’t seem inclined to use the hint at all, but o4-mini-high gave a valid informal proof. So we have to wonder: how far out could “ab+1” be in o4-mini-high’s distribution anyway? I wouldn’t be surprised if only a bit more training would help it find this sort of idea, although perhaps I’m underestimating how hard it is to get a training signal on even slightly non-trivial informal proofs. In any case, I think this supports the idea that this problem doesn’t require too much insight.

Turbo the Snail (P5)

This is my favorite recent problem: it requires essentially no math background but is still plenty challenging.

The problem statement is long, but not complicated. The top and bottom rows have no monsters. The other 2022 rows each have one monster. Since there are 2023 columns, “at most one monster per column” means there’s a single safe column and each other column has one monster. The question is, what’s the fewest number of attempts Turbo needs to get from (say) the top row to the bottom row?

2023 is sufficient: go straight down each column, and eventually you’ll find the safe one—though it might be the last one you try, if you get unlucky. Can you do better? Playing around, there are some promising patterns. For instance, if you ever find two monsters in adjacent columns that are not in diagonally adjacent cells, then you can zigzag around them. But, of course, the monsters could all be in diagonally adjacent cells: they could be in one big diagonal running from (say) the top left to the bottom almost-right, with the rightmost column being the safe one—thus eliminating the promising pattern. Of course, maybe there’s a cleverer strategy that would take advantage of that diagonal pattern…

That’s just the start, but it shows the style of thinking you have to engage in. Really, that’s the only way to approach it: there’s no math background to apply so, you, like Turbo, are on your own on the grid. This is one aspect of the elusive concept of creativity: you must understand the problem de novo, without guidance. It’s the understanding that you’re creating. Also, on this problem, the final answer is somewhat counterintuitive. Anyway, I’m still reluctant to really spoil it in passing, but if you’d like to see the solution, I recommend page 12 here.

AlphaProof made no progress on this problem. In fact, apparently it took the humans on the GDM team over a day to even express the problem in Lean. Mathematician Timothy Gowers—who was involved in AlphaProof to some extent—mentions one reason why.

Source

One approach to formalizing a “strategy” would be to first formalize an “attempt” and a “monster knowledge state”, and then define a strategy as a function from pairs of sets of attempts and monster knowledge states to attempts. That is, the strategy function takes the set of attempts made and the knowledge about monster locations gained from those attempts, and returns the next attempt to make. An attempt can just be a path through the grid, and a monster knowledge state can just be a set of cells. Then, you have to define what it means for a strategy to guarantee winning in a certain number of attempts. You can see how this might be a bit gnarly! If you’re curious, a full formalization can be found here.

In any case, it must have been a bad fit for the existing structures in Lean if the GDM team couldn’t formalize it right away. And if it’s hard to formalize the statement, it seems likely that it’s hard to prove it as well. As Gowers says, for whatever reason—social evolution? it’s fun to speculate—we find these “strategy” objects pretty natural to think about, even though we don’t find them particularly easy to formalize.

This sort of gap between intuitive and formal reasoning is one of the challenges of formal approaches: it might turn out that you need a lot of pre-work before an FPM is in any position to solve a particular problem. What we might really dream of is an AI system that can help solve the pre-work part of the problem too, but that’s a whole different ball game.

This also raises the possibility that, for some problems, it might be easier for RLLMs to generate informal proofs than for FPMs to generate formal proofs. P5 doesn’t give much evidence either way, though: RLLMs also make no progress on it, not even if given the right answer and just tasked with finding a strategy that guarantees a win in that number of attempts.

I should also mention that the diagrammatic/geometric reasoning required to solve this problem may be an extra barrier for RLLMs and FPMs alike. This is certainly the only way a human would solve it, visualizing or sketching different paths through the grid, but we’ve speculated before that RLLMs may be weaker at this kind of reasoning. Even a formal solution, which wouldn’t rely on a diagram directly, might be hard to derive without a diagrammatic model “in mind”, so to speak.

Incidentally, P5 is another problem that isn’t provable as stated: you have to prove that the answer is some specific integer. You know that the answer must be a positive integer less than 2024, though Hubert’s slides say they only generated on the order of 100 candidate answers. Numerically speaking, at least, it seems possible that they might have missed the right answer in this step. For what it’s worth, I tried a simple prompt with o4-mini-high, asking it to generate 300 high-probability candidate answers—and it failed to include the right answer. I didn’t see any discussion of this issue from GDM one way or another.

Aquaesulian Functions (P6)

This seems like AlphaProof’s crowning achievement. Only five contestants got a full score on this question. It is inarguably difficult.

The 2024 IMO was held in Bath, UK. The Roman name for Bath was Aquae Sulis. “Aquaesulian” is not otherwise a term used in math.

This is called a “functional equation” problem because the core relationship is an equation relating values of a function, and you must prove something about functions that satisfy the equation. It’s a common type of math olympiad problem. What makes this one a bit unusual is the “or”: instead of a single equation, we’re told that one of two equations always holds. This gives us a lot to keep track of, which is part of what makes the problem hard.

I’ll very roughly sketch the first half of a human solution, in order to make two points. First, with functional equation problems there are many standard approaches to try, and many of them yield some initial results on this problem. Second, part of what makes this problem hard is that it is deep: you have to accumulate a lot of intermediate results, and the results build on each other. This makes the problem especially hard when under time pressure, as on the IMO. Still, I would venture to say that there’s nothing too tricky here: it’s more that you just have a lot of ground cover, and you can spend a lot of time in dead ends.

Let’s take a look at how you might get started. One standard technique is plugging in specific values. For instance, if you plug in x=y=0 here, you get f(f(0)) = f(0). That’s not much, but you tuck it away as a small intermediate result. Another thing that is often fruitful is seeing if you can show that the function is injective or surjective. In this problem, if you play around with the functional equation, you can get injectivity without too much trouble. That, together with the first result, gives f(0)=0. From there, you might as well try surjectivity. Here you need to think to set y=f(-x), which isn’t obvious by any stretch, though the f(r)+f(-r) part of the problem might seed the idea. Once you’ve got that, you can use injectivity to show that f(-(f-x))=x in general, which implies surjectivity.

Now you can turn to the f(r)+f(-r) part in earnest. Since f has an inverse, you know that f(-x) = -f⁻¹(x). Thus, you want to find the maximum number of values that f(x)-f⁻¹(x) can take on. Clearly it is 0 when x=0. Can it take on any other value? In fact the answer is that it can take on at most one more value, so the final answer is 2. I’m not sure how you’re supposed to guess that. I wouldn’t be surprised if AlphaProof didn’t guess it for any smart reason: you’d just be foolish not to have 2 among your hundreds of candidate answers.

I won’t sketch the rest, which is arguably harder as it doesn’t follow any standard techniques: you just have to apply the functional equation just right and track the possibilities introduced by the “or”. And you also have to produce an example of an aquaesulian function for which f(r)+f(-r) takes on two values. Nothing comes trivially. For a full solution, I recommend Solution 1 on page 25 here.

If P5 was a bad fit for formalization, maybe P6 is a good fit: what are theorem provers good at if not keeping track of logical operators! What’s more, if depth is one of the big factors that makes it hard, then MCTS might be an especially good fit as well.

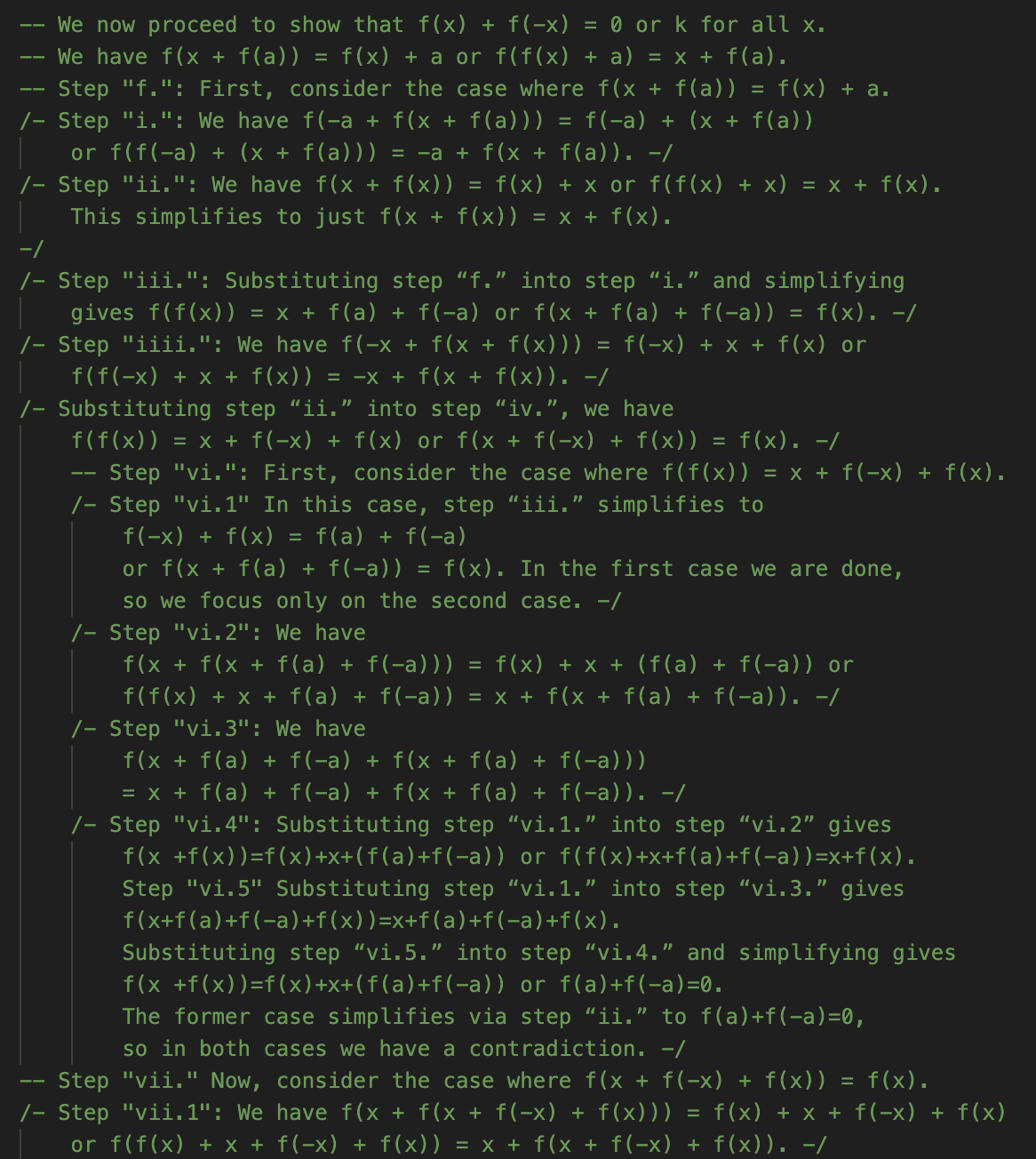
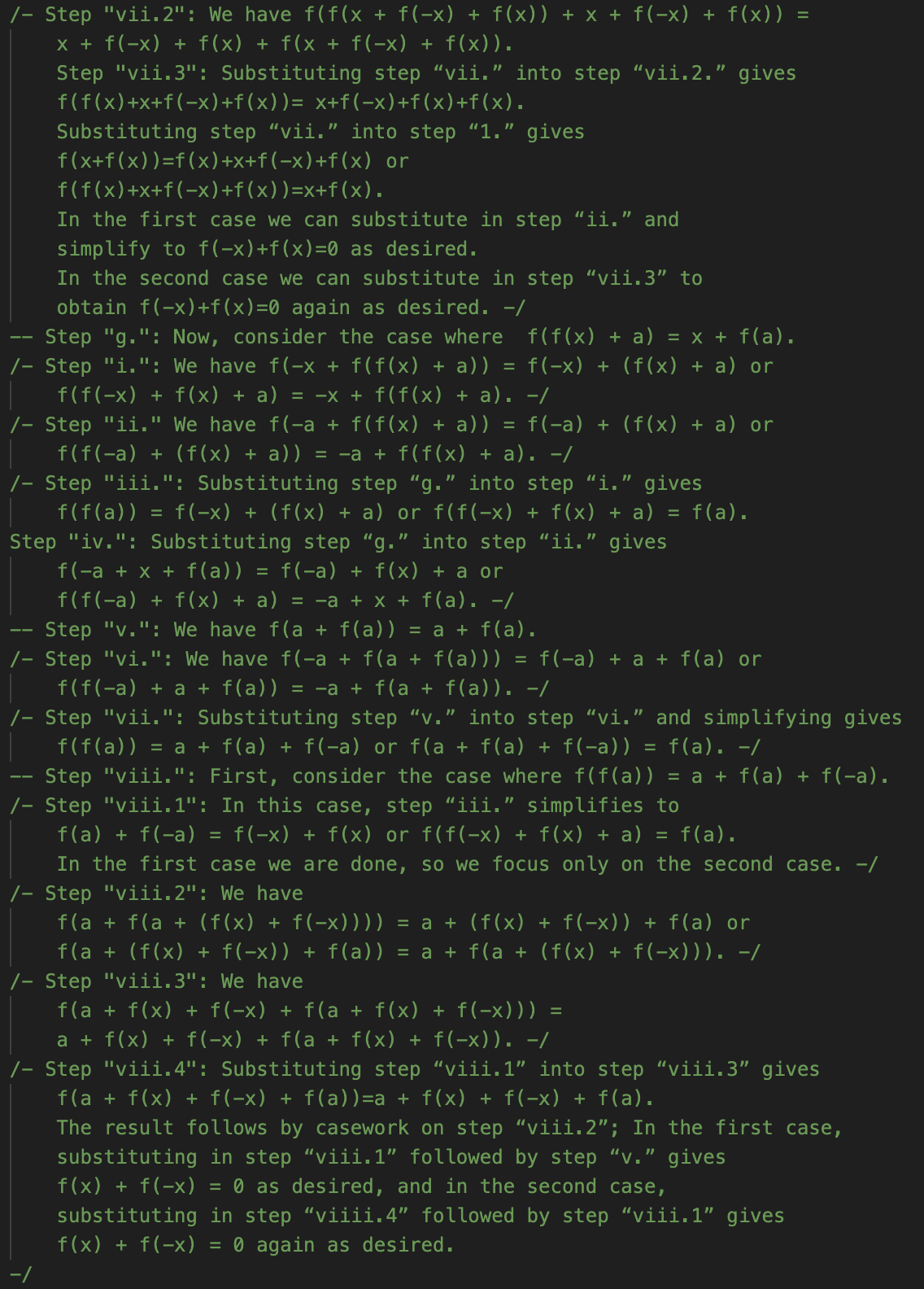
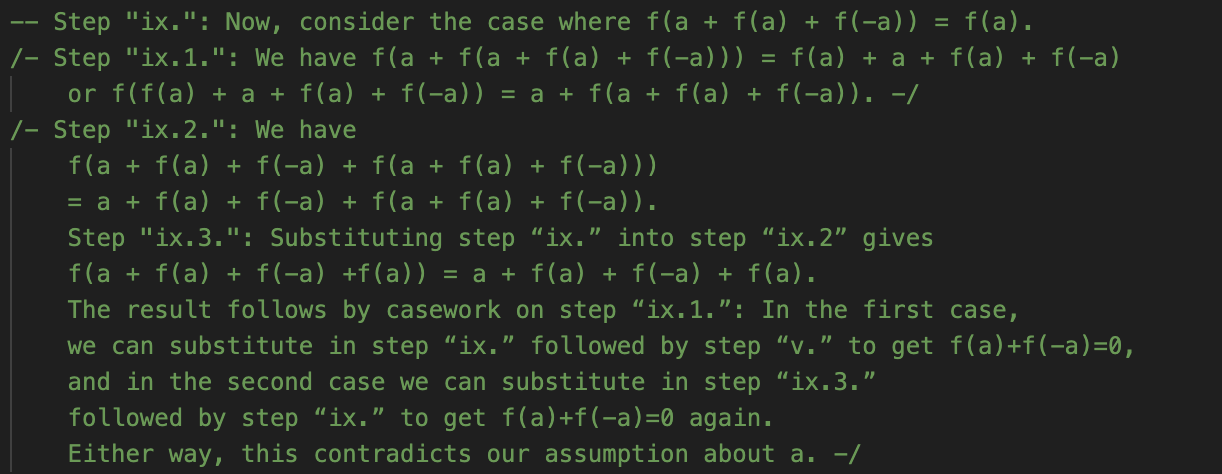
Too true, perhaps. AlphaProof’s solution does not look like what I sketched above, or any other human solution I’ve seen. As far as I can tell, it doesn’t prove anything general about f, but instead works through a very lengthy set of cases. GDM helpfully added informal comments, which I’ll show for the core of the proof below. I don’t intend for you to read these in detail! But give it a skim to get a feel for what is and isn’t present. Recall that it’s taking for granted that the answer is 2 and trying to prove that. In this notation, f(a)=k.

I’m suspicious of myself for saying this about what is clearly an impressive headline result, but this is about as low of a “low road” as a solution could possibly take. It is highly reminiscent of some of the grind-it-out solutions we’ve discussed from RLLMs. I had suspected that, if anything made P6 more approachable, it would be that there are standard techniques to get started on functional equation problems. That doesn’t look like what AlphaProof is doing. Instead, it’s just applying the functional equation over and over, leading to a profusion of individual cases—all of which it manages to, eventually, run to ground.

Is there a reason both RLLMs and AlphaProof have “low road” tendencies? Maybe. Both are trained with reinforcement learning, which can use “outcome” rewards or “process” rewards. Outcome rewards derive a signal from whether the system gets the right answer. Process rewards derive a signal from whether the system takes the right steps to get the right answer. If the designers of these systems used process rewards, they would presumably target nicer-looking proofs than the above—but as far as we know, they are all using outcome rewards. Thus, if it so happens that “low road” solutions are easier for the system to learn how to find, then it will have no reason to find anything else.

Anyway, if this is the only kind of “hard” problem that these systems can get, i.e. ones amenable to such grinds, then I think we really have to say that the system is not showing signs of doing interesting math.

Beyond interestingness, this also limits mundane utility. Unlike with P2, the issues with AlphaProof’s solution to P6 are deeper than “code cleanup”: a human mathematician would not want to engage with the conceptual structure of this proof if they could at all help it. It’s fine to treat the theorem as a black box result: trust that it’s true and move on; there’s a place for that. But it’s a bigger issue, in terms of human-computer interaction, if humans want the AI system to shed some light on why the statement is true, and all the AI system can say is, “Well, I checked a bunch of cases, and it is.”

Counting Numbers (P3)

Difficulty-wise, P3 is in the same ballpark as P6. Only eight contestants got a full score on it. IMO coach Evan Chen rates it one click harder than P3. I wouldn’t make too much of the differences: these problems are both very hard.

You have a sequence that starts with N arbitrary positive integers. After the Nth one, a rule kicks in: the next number is the number of times the previous number has appeared already in the sequence. I like this problem because it’s the sort of thing you might invent while just messing around, similar to the look-and-say sequence. It’s neat when such mathematical doodles end up having interesting structure to them.

There are a number of great discussions of this problem. One is from Steve Newman, a former IMO competitor himself, who writes not just about his solution but about his problem-solving process. Another is this video, which puts in the work of explaining every step of the solution very clearly and with nice visuals—the 40 minutes fly by. Finally, Chen’s written solution starts on page 6 here.

The first thing to note about the solution is that, as with P6, it’s deep: you have to build up lots of intermediate results. Here, for instance, are the six key steps of Newman’s solution (lightly edited):

1. There is an M such that any number greater than M appears at most M times.

2. The number 1 appears an infinite number of times.

3. All of the numbers that appear an infinite number of times are adjacent.

4. Let k be the largest number that appears an infinite number of times. Then we can find some number K such that all numbers >K appear at most k times.

5. Things eventually settle into an alternation of large and small numbers. Once all numbers from 1 to k have appeared at least K times, the sequence alternates between numbers no larger than k and numbers larger than K.

6. Across all positions in the sequence, there is a finite upper bound on the difference between the number of times each of the infinitely-repeating numbers (numbers in the range 1…k) have appeared.

Each of these steps requires proof, and there also must be a final argument that, taken together, this implies the desired result. Clearly there’s a lot of work to do here.

Second, as with P5, you don’t have much guidance on how to try to find these steps: you just have to play around and create your own understanding of what’s going on. This is a bit different from P6 and its functional equation: you can do something with a functional equation, and indeed AlphaProof does a whole lot with it. It’s not clear at first what to do with this sequence.

Finally, all solutions I’ve seen invent some sort of book-keeping method, usually visual, to manage the information about the sequence. Here’s the one Chen uses.

After block N, 4 has appeared once, so the next block, B₉, is added to tower 1. At that point 1 has appeared twice, so B₁₀ is added to tower 2. At that point 2 has appeared six times, so B₁₁ is added to tower 6 — and so on.

This seems very useful: proofs of the intermediate steps reference this diagram over and over. I think this points to another aspect of creativity: the invention of structure. At least for humans, figuring out how to organize information can be the key element to solving a problem, even if that organizing mechanism might not be strictly required in the final proof. And really the sky’s the limit here: mathematicians spend decades inventing whole edifices of structure, in the hope that they will at last allow them to solve big problems. Some mathematicians would say that’s the whole ballgame.

Such structures can be hard to formalize, though informal representations also have their drawbacks. Reading some online commentary on P3, it sounds like some people got onto roughly the right track, but when using informal reasoning devices like the diagram above, it can be easy to bluff over the details. No such fooling yourself in formalization, though you may have to do much more work.

I don’t know how this will play out for AI systems: maybe they end up getting away without this sort of reasoning aid, at least sometimes, or maybe they have to learn how to create them. If the latter, we might even speculate that it will be pretty hard to do that with only the sparse signals of outcome-based reinforcement learning. There certainly aren’t any signs that they’re getting close to it today.

Hubert says they thought AlphaProof might have been getting close to a single point of partial credit on this problem by proving some intermediate result. They let it run for an extra day, but, in the end, it didn’t get anywhere.

IMO Conclusion

What do we make of AlphaProof? When it came out, I assume that the fact it was generating formal proofs at all was quite impressive. Now, though, we know that reinforcement learning on top of language models can go pretty far so long as there is easy access to a reward signal—which, in the case of formal proofs, there is.

Does it solve problems of greater mathematical sophistication than other systems? P2 shows it can get some “single trick” problems that are beyond current RLLMs—though perhaps not too far beyond them. P6 is an impressive achievement, but the solution itself is a bit of a letdown. It’s a small sample, but I find it underwhelming: when it comes to creative problem-solving, we see some of the same gaps we’ve seen from RLLMs.

Looking ahead, I do think AlphaProof would do well on some existing benchmarks, if GDM ever tries it out. For example, PutnamBench seems ripe for a strong showing. Putnam problems are roughly comparable in difficulty to IMO problems, maybe even requiring a bit less creativity, but the current top performance on PutnamBench is only 1.5%. Then again, that might just be a matter of compute: I doubt that the models currently on the PutnamBench leaderboard ran for days on each problem the way AlphaProof did. As for the IMO, I don’t have a strong sense for how likely it is that a scaled-up AlphaProof would ace it, but I do think it would be a clear step forward, especially if it involves solving problems that don’t admit “low road” approaches.

1. One experiment you could run would be on games, which also have readily available reward signals. If you make an RLLM that is post-trained to play go, I assume it will get better at go. Can it get as good as GDM’s AlphaGo? If so, does it use data and compute more or less efficiently? I’d bet on AlphaGo winning, but the degree of the gap would be instructive.

2. Rather than start with natural-language problems I suppose you could try generating completely random Lean statements for this step? I imagine you would mostly get trivialities, though. And, anyway, you do want problems in the broad ballpark of competition math problems, if that’s what you’re ultimately going to test on.

3. It’s unclear to me whether they started with a broad-based language model and further trained it on Lean’s Mathlib, or if they trained it on Mathlib from scratch.

4. Many natural languages, in fact! It’s the International Mathematical Olympiad, after all.

5. Two caveats when interpreting these numbers. First, because each country sends a team of six regardless of that country’s size, we wouldn’t expect the contestants to be the most mathematically talented high school students in the world. It seems likely that the seventh-best student from China—who just missed the cut for China’s team—is stronger mathematically than the sixth-best student from Iceland. Second, the difficulty of the final problems on each day is well-known, and thus might be a bit of a self-fulfilling prophecy. Unless you’re really going for the gold, it might make more sense for you not to even attempt P3 or P6, if you think your time could be better spent making progress on the easier problems. A lot of the 0’s on P3 and P6 might be blank solutions.

6. Observe that, bending the rules a bit, if you set n=-1, then both terms, 1/a+b and a+1/b, have numerators divisible by ab+1. You can’t set n=-1, so instead you want a value of n>N where a^n and b^n are congruent to 1 (mod ab+1). This ensures that a^(n-1) and b^(n-1) are congruent to a^(-1) and b^(-1), and it turns out that you still get divisibility by ab+1. See the Remark on page 4 here.

7. In fact, AlphaProof had to run for a few days before it found a valid proof. Still, I don’t hold that against it too much: both because it can presumably be made to run faster with “mere” engineering, and because, even if we did sample an RLLM a thousand of times, we wouldn’t have a good way to tell if the outputs were 99.9% junk or 100% junk.