Gemini 2.5 Pro Picks the Low-Hanging Fruit
Think of its math abilities like o3-mini-high with some kinks ironed out
Gemini 2.5 Pro, the latest model from Google DeepMind (GDM), came out at the end of March. It scores better on several math benchmarks than all prior models. This is the first time since I started this blog that there’s been a new “best math model”, a mantle previously held by o3-mini-high. While the headline numbers speak for themselves, I’ll use this post to redo some of the more qualitative analysis from prior posts to better characterize the nature of the advance.
TL;DR: When evaluating o3-mini-high, I’ve noted that some of its errors don’t feel particularly fundamental: a bit more training or even just “thinking time” might yield straightforward improvements. Gemini 2.5 Pro seems to have improved on precisely these fronts. It makes fewer mistakes, allowing it to grind out out longer solutions. It has a better sense of what a proof should look like, allowing it to produce more valid proofs on its first try. It has a better memory, recalling specific results and their proofs; this probably makes it more useful, though it also makes data contamination more of a live issue. Beyond that, it is largely similar to prior art: it doesn’t solve fundamentally harder problems and it isn’t able to solve problems in new ways. In other words, the progress is incremental rather than revolutionary.
While the capabilities might not be so I novel, I do think this represents something new in the competitive landscape: it’s the first LLM-based system whose math abilities are clearly ahead of OpenAI’s o-series. The competition had been playing catch-up here since last fall—and hadn’t quite gotten there. DeepSeek-R1 was impressive for being built at lower cost, but was still a bit less accurate. Claude Sonnet 3.7 might have been (and might still be) the best at coding, but is not better at math. You had to wonder if OpenAI had some magic when it came to staying ahead of the pack in math. There wasn’t any deep reason to believe this, but it felt like a live hypothesis. Gemini 2.5 Pro is some concrete evidence that it isn’t so.
Headlines
First, a quick summary comparison of Gemini 2.5 Pro and o3-mini-high. Here are their scores on the three math competitions covered on MathArena. These competitions all took place in 2025, and, as far as I can tell, Gemini 2.5 Pro doesn’t know about anything from late 2024 onward, so data contamination shouldn’t be an issue.1
So: identical on the AIME and ≈20 percentage points better on the other two. What accounts for the jump?
New Highs in Low Roads
I’ve written before about how models consistently take the “low road” to solving problems: rather than finding a clever insight or more deeply understanding the structure of a problem, they grind out long computations. This is often something a human simply can’t do in a timed competition, but speed is much less of an issue for computers. However, the longer the computation, the more likely the model is to introduce a “careless” mistake and eventually get the wrong answer.
A big part of Gemini 2.5 Pro’s headline improvement seems to come from letting fewer mistakes slip through. It’s still taking the low road, it can just go for longer without straying.
Anything You Can Do I Can Do Better, But If You Can’t Do It Then Neither Can I
One way to see this is that there are very few problems on MathArena which o3-mini-high never solves but which Gemini 2.5 Pro sometimes solves.2
For example, on HMMT, there are 12 problems where Gemini 2.5 Pro does better than o3-mini-high, but on only two of these did o3-mini-high score a flat zero. Of those two, I previously discussed one as being especially idiosyncratic, out of line with o3-mini-high’s general capabilities. I’ll mention the other below.
Improved Coordination
The distinction is especially clear on geometry problems, which often have both high- and low-road solutions. The high road often involves introducing a new element to the setup—e.g., a new point or line—which can greatly simplify subsequent computations. The low road involves putting everything in a coordinate system—e.g., the Cartesian plane—and then slogging through a morass of algebra to get the answer. This latter approach is called a “coordinate bash”: you bash the problem with coordinates until it cracks.
Gemini 2.5 Pro is better at coordinate bashes than other models.
One example of this is the 5th geometry problem from HMMT, which I discussed in a previous post. You can see the full problem there, but, in brief, the high road involves adding a single well-chosen point, after which there’s a quick path to the solution. Instead, though, the models all go for coordinate bashes: o3-mini-high gets this right 1/4 times, whereas Gemini 2.5 Pro gets it right 3/4 times.
Another example is the 10th geometry problem from HMMT. This is the other HMMT problem I mentioned above, which Gemini 2.5 Pro sometimes got (3/4 times) but o3-mini-high didn’t get at all. Similarly, the intended solutions involve conceptual reasoning about the shapes, but Gemini 2.5 Pro just bashes it.
Finally, this also accounts for part of the USAMO results. P4, the easiest problem on the second day of the competition, is a geometry problem.3 The USAMO requires proofs, but proofs are sometimes amenable to bashes: you set up coordinates and use algebra to try show the desired geometric property. Among prior models, one (DeepSeek-R1) had gotten most of the way to a coordinate bash 1/4 times. Gemini 2.5 Pro, on the other hand, gets all the way there 2/4 times.
Prove It
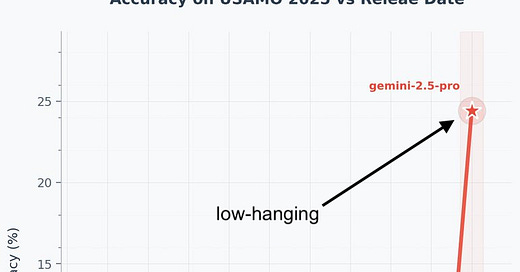
The USAMO is the one place where it might look like Gemini 2.5 Pro has broken new ground. Prior models all scored less than 5%, but it scored 24%. Is that a “zero to non-zero” scenario?
I don’t think so. Shortly before MathArena released its evaluation of Gemini 2.5 Pro, I wrote a post whose whole thesis was that non-zero performance on the USAMO was basically already baked into existing models.
The thesis of this post is that a model like o3-mini-high has a lot of the right raw material for writing proofs, but it hasn’t yet been taught to focus on putting everything together. This doesn’t silence the drum I’ve been beating about these models lacking creativity, but I don’t think the low performance on the USAMO is entirely a reflection of this phenomenon. I would predict that “the next iteration” of reasoning models, roughly meaning some combination of scale-up and training directly on proofs, would get a decent score on the USAMO. I’d predict something in the 14-28 point range, i.e. having a shot at all but the hardest problems.
Sure enough, the USAMO question that Gemini 2.5 Pro did best at is P1, which is also the one where I had the easiest time “coaxing” a proof out of o3-mini-high.
Of course, it only got this proof with my prompting. Even so, I would say it still did most of the heavy lifting. My questions were all “playing dumb”: I didn’t supply any new ideas, I just drew its attention to the steps in its argument that I believed were wrong or weak. In fact, I think I played a role similar to what we see it do on its own in its chain of thought: repeatedly asking, “Wait, is that right?” So while it clearly needs assistance to do this today, I don’t think the capability is far beyond it. Heck, I’d even be curious what happens if you just let it think for longer — a parameter we can’t control, beyond choosing “high” reasoning mode.
It seems as good a guess as any that GDM is “letting it think for longer”, and that this accounts for some of its improvement. It also seems like Gemini 2.5 Pro just has a better grip on what a proof is supposed to look like. As I discussed in the prior post, o3-mini-high would break some “genre rules” of proofs, ranging from failing to mention when it didn’t use a premise to bluffing over steps where it didn’t have an argument. Gemini 2.5 Pro doesn’t do that as much—which, in the case of bluffing, is a welcome relief. But I’d say that this part of its USAMO performance is due to getting the style right, rather than having much new substance.4
So, you might see this chart floating around, but I don’t think reality is as dramatic as the trend indicates. I think this is picking the low-hanging fruit, not a new capability.

A Glimmer?
The one other bit of progress Gemini Pro 2.5 made on the USAMO was on the much harder P3, which I also discuss in the prior post. It doesn’t come close to solving the problem, but, one time out of four, it hit on the key construction to start with. This is not easy for a human. Still, I wrote:
That’s one ray of hope: the construction […] isn’t that complicated, and once you start playing with it, you realize it fits into the problem nicely. The other bit of hope, for an AI system anyway, is that there’s some prior art here: the [construction] is an example of an object called a Gabriel graph, which has been studied extensively.
[…]
This problem requires more creativity than the prior two. Even so, I’m not even sure I’d say it requires a lot of creativity. Hitting on the construction seems like the main challenge, but the construction itself has a concise description. There are some plausible paths there too, especially if your background knowledge includes Gabriel graphs.
Sure enough, Gemini 2.5 Pro referenced Gabriel graphs when coming up with the construction, even though it wasn’t able to make any more progress after that. So, even if it were to get this problem, that might be as much due to background knowledge as to an ability to do de novo math.
To sum up, its better handle on proofs lets it solve the easiest USAMO problems, and it doesn’t make progress on the harder problems. I think a perfect score on the USAMO would represent something qualitatively new, but Gemini 2.5 Pro has taken only a small step in that direction.
If I Recall Correctly
In a previous post, I discussed how o3-mini-high’s memory is weaker than I expected. It can’t recall famous IMO problems or their solutions—or famous poems, even.
Gemini 2.5 Pro seems better on these fronts.56 As I’d done with o3-mini-high, I asked Gemini 2.5 Pro to recall the statement of Problem 6 from the 1988 IMO, a notoriously difficult problem that has been discussed a great deal. Unlike o3-mini-high, Gemini 2.5 Pro was able to recall the statement—as well as a full solution.
In fact, it was able to solve the problem even if I didn’t mention its source. Since this problem’s difficulty seems far beyond that of the newly-released problems that it can solve, we must conclude that it can memorize solutions it has seen during training.
Combined with its better handle on proofs I suspect this will make it significantly more useful as a tool for learning and doing math. Unfortunately, it also means we can’t meaningfully test it on historical problems. The above example is probably already enough to scare us off of that, but, just to see, I repeated the same experiment I described in the post on data contamination.
The idea was, if you filter to hard IMO problems with short-form answers, and control for how “guessable” the answer is, you can see relatively easily whether the model has memorized the answers. o3-mini-high got only 2/9 of the problems I assessed to be not too guessable, suggesting its memory for such solutions isn’t very strong.
Gemini 2.5 Pro got 6/9 of them. I didn’t check the proofs in detail, but it wouldn’t surprise me if some were correct, as with P6 from the 1988 IMO. It might also be better at guessing: its “low road” skills might open up new ways for it to work out patterns from small examples.
So, no way around it: Gemini 2.5 Pro has a good enough memory that apparent solutions to hard problems might just reflect it having seen the problems before. This effect isn’t black-and-white, but it’s plausible enough in any given case.
I’m Afraid I Can’t Do That
One funny consequence of this is that Gemini 2.5 Pro can recognize unsolved problems, and it doesn’t seem to believe in itself enough to attempt them. I gave it an open problem—obscure enough that I hadn’t heard of it before, though of course not at all obscure in its field—and it had this to say.
In contrast, given the same problem, o3-mini-high charges in wildly and makes a mess. Maybe not as helpful, but, you know, I respect the chutzpah.
Drawing Conclusions
Humans often draw diagrams when solving problems: “a picture is worth a thousand words” applies in math too. Language models aren’t good at this: they prefer words. Gemini Pro 2.5 is no different.
I’d previously written about how o3-mini-high couldn’t solve a relatively easy combinatorics problem on HMMT, and speculated that it was due to the way the solution relies on drawing the right diagram and then basically just starting at it until you see what’s going on. There’s no viable low road alternative.
Gemini 2.5 Pro also whiffs on this question. To be fair, it seems to know that it’s lost: 2/4 times it just writes some Python code! The code gives the right answer, but Gemini Pro 2.5 can’t execute it. It tries to imagine the output, but, no luck.

I’ve also written about an algebra problem that is actually a geometry problem in disguise. Here there is a clear high road vs. low road: either you recognize the hidden geometry, or else you grind through the algebra. o3-mini-high was completely sunk on this problem. Gemini 2.5 Pro actually got it! But only via the low road.
I’ve also written about my current favorite hard problem for testing AI systems, P5 from the 2024 IMO. It’s more like a riddle than anything: you need no math background whatsoever, but you do need to think really carefully about the dynamics of moving around the grid specified in the problem. It also has a solution that’s easy to check and, as far as I’ve seen, hard to guess. Gemini 2.5 Pro doesn’t get it.
Rate Your Own Proof
If it has a better grasp on proofs, can it tell when its own proofs are incomplete or wrong? I gave it P2 from the 2025 USAMO—a problem where it has a flat 0/7 on each of 4 runs on MathArena. It’s pretty transparent that it’s not really giving a proof:
So, in a fresh session, I gave it the problem and its own solution (described as “one contestant’s solution”), and asked to predict what score the solution got. It said 6/7, deducting only 1 point for this gap which is, in fact, basically the whole problem.
I’ve written before about how, if a model can rate its own proofs, then we could have it try to solve a large collection of unsolved math problems, and at least filter out the obvious failures. With Gemini 2.5 Pro I’m more optimistic that something like this can be made to work, but it doesn’t seem like it solves it right out of the box.
Update: in a subsequent post, I tried a bit harder here and got decent results. Gemini 2.5 Pro shows some promise at filtering out its own bad proofs.
Predictions
When it comes to making stuff up, language models shouldn’t get to have all the fun. So, here are a few predictions.
Both the dedicated low-road guessing and better memory seem like they would improve performance on FrontierMath. I predict that Gemini 2.5 Pro will outscore o3-mini-high in an apples-to-apples setting run by Epoch AI. (95% CI of 10-40%, with the mode at 20%)
The USAMO has roughly comparable difficulty to some other high-profile math competitions like the IMO and Putnam. Gemini 2.5 Pro will do comparably: getting the easier questions and not the medium-to-hard questions. (95% CI of 1/6-1/2)
The next generation of models won’t ace these competitions. (95%)
Mathematicians generally find Gemini 2.5 Pro to be the most useful, of currently-available models, for assisting in math work. To be fair, I’ve already seen a couple comments to this effect. (75-95% range, depending on operationalization.)
Prediction 3 seems boldest to me. There’s a “straight lines on graphs” case for acing these competitions, and it hasn’t paid to bet against that sort of thing. Still, I see very little evidence of any model breaking into the hardest tier of elite olympiad problems. One thing I’m less sure of, though, is this conditional: if the next generation of models (o4, say) hits the upper end of my expectations by getting the easier half of elite olympiad problems, what is the probability of the subsequent generation acing these tests? You can debate the slope of the straight line, after all.
I don’t have an opinion here yet. One way to approach it would be seeing if you could break down the hardest problems into solving a series of medium problems. That’s conceptually appealing but not obviously true, I think. Something for a future post!
For instance, if ask for “today’s date” it tends to give a date in May of 2024. If ask who is president of the US, it says Joe Biden.
Recall that MathArena poses each problem four times, which lets us get a sense for how frequently each model solves each problem.
It seems relevant to note that the AlphaProof team is also at GDM, but I’m not sure what to make of that. On the one hand, if GDM did train Gemini 2.5 Pro specifically to be better at writing proofs, maybe some of AlphaProof expertise is at play. On the other hand, Gemini 2.5 Pro isn’t really writing hard proofs–it certainly is worse than AlphaProof–so maybe there isn’t so much expertise to transfer.
A censor layer is preventing Gemini 2.5 Pro from reciting the same poem I tested o3-mini-high on, but the Declaration of Independence shows a similar pattern: Gemini 2.5 Pro recites it to the letter whereas o3-mini-high makes some minor errors.
As far as I can tell, it doesn’t have a static snapshot of the web the way o3-mini-high does. The user has control over whether it has the ability to use Google searches, and I left that toggle off in all of these explorations.